在层次分析模型中,成对比较阵最大特征根对应的特征向量可作为层次分析模型的决策向量()
A. 正确
B. 错误
查看答案
相关试题
换一换


层次分析模型中,成对比较阵最大特征根对应的特征向量可作为层次分析模型的决策向量。
答案
在层次分析模型中,成对比较阵最大特征根对应的特征向量可作为层次分析模型的决策向量()
A.正确 B.错误
答案
正互反矩阵A的最大特征根必为正实数,其对应特征向量的所有分量均为正实数。
答案
设A是n阶矩阵,λ是A的特征值,其对应的特征向量为X,证明:λ^2是λ^3的特征值,X为特征向量,若A^2有特征值λ,其对应的特征向量为X,X是否一定为A的特征向量?说明理由.
答案
设A为n阶方阵,α为A的对应于特征值λ的特征向量,β为AT的对应于特征值μ的特征向量,且λ ≠ μ,证明α与β正交
答案
层次分析法中,如果满足一致性,判断矩阵的特征向量就是权重向量。
答案
当特征值为单根时,对应的线性无关特征向量个数只能是一个.
答案
设列向量p=[1,-1,2]T是3阶方阵相应特征值λ的特征向量,则特征值λ等于()
A.3 B.5 C.7 D.不能确定
答案
已知二阶实对称矩阵A的特征值是1 , A的对应于特征值1的特征向量为(1, - 1 ) T,若|A|= . -1,则A的另-一个特征值及其对应的特征向量是( )。
A.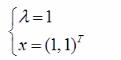 B.
B.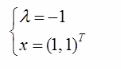 C.
C.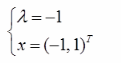 D.
D.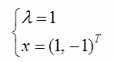
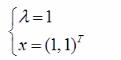 B.
B.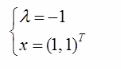 C.
C.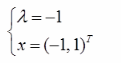 D.
D.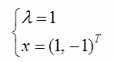
答案
【 】可用来计算矩阵的按模最大的特征值和特征向量
答案
热门试题
应用层次分析法解决方案评价问题的主要困难在于矩阵特征值和特征向量的计算。
A的实特征向量所对应的特征值的绝对值等于1.
设A是3阶矩阵,是A的属于特征值1的特征向量,是A的属于特征值-1的特征向量,则()
若方阵A可以对角化,则A的每个特征值的重数等于该特征值对应的无关特征向量个数
已知α=的一个特征向量,则( )。
幂法的基本思想是构造一个向量序列使之逼近主特征值对应特征向量,然后求出主特征值。那么,主特征值是( )
乘幂法主要是用来求矩阵的主特征值(按模最大的特征值)及相应的特征向量。()
求解矩阵A的特征值和特征向量的R命令是()
若λ为矩阵A的k重特征值,则对应于λ的线性无关的特征向量的个数不超过k()
中国大学MOOC: 实对称矩阵A的不同特征值对应的特征向量不仅是线性无关的而且是
设λ1,λ2是矩阵A的两个不同特征值,a,β分别为A对应于λ1,λ2的特征向量,则a,β()
当特征向量导入解码器后,会通过,计算出概率最大的音素
设λ1,λ2是矩阵A的两个不同的特征值,α,β分别为A对应于λ1,λ2的特征向量,则α,β()。
若λ为矩阵A的k重特征值,则对应于λ的线性无关的特征向量的个数一定等于k()
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
设A是3阶实对称矩阵,Р是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值入的特征向量,则B的属于特征值A的特征向量是()
主成分分析的步骤顺序是。①确定主成分②求出协方差矩阵③对原来的指标进行标准化④求出协方差矩阵的特征根和特征向量()
设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有
特征向量α就是齐次线性方程组



 使用微信扫一扫登录
使用微信扫一扫登录