在线性回归模型中,若解释变量X1和X2的观测值成比例,既有X1i=kX2i,其中k为非零常数,则表明模型中存在()。
A. 异方差
B. 多重共线性
C. 序列相关
D. 随机解释变量
查看答案
相关试题
换一换


在线性回归模型中,若解释变量X1和X2的观测值成比例,既有X1i=kX2i,其中k为非零常数,则表明模型中存在()。
A.异方差 B.多重共线性 C.序列相关 D.随机解释变量
答案
若P(X≤x2)=0.6,P(X≥x1)=0.7,其中x2>x1,则P(x1≤X≤x2)的值为()。
A.0.6 B.0.7 C.0.1 D.0.3
答案
已知x1,x2为整型变量,x1的值为65,x2的值为97,执行printf(“%d,%c”,x1,x2)的结果为()。
答案
以货物周转量Y为因变量,国内生产总值X1和运输线路长度X2自变量,建立二元线性回归模型,该模型的形式是()
A.Y=β0+β1X1+β2X2 B.Y=β0+β1X1+β2X2+ε C.E(Y)=β0+β1X1+β2X2+ε D.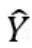 =β0+β1X1+β2X2+(选项不全)
=β0+β1X1+β2X2+(选项不全)
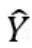 =β0+β1X1+β2X2+(选项不全)
=β0+β1X1+β2X2+(选项不全) 答案
对于下述语句,分别将12和34赋给变量x1和x2,则应按()方式输入数据。int x1,x2;scanf("%d%d",&x1,&x2);
A.) 1234 B.) 12 34 C.) 12,34 D.) 12
答案
己知函数y=f(x)在x1和x2处的值分别为y1和y2,其中,x2>x1且x2-x1比较小(例如0.01),则对于(x1,x2)区间内的任意x值,可用线性插值公式( )近似地计算出f(x)的值。
A.y1+(y2-y1)(x-x1)/(x2-x1) B.x1+(y2-y1)(x-x1)/(x2-x1) C.y2+(y2-y1)(x2-x1)/(x-x1) D.x2+(x2-x1)(x-x1)/(y2-y1)
答案
中国大学MOOC: 设有n维随机变量(X1,X2,…,Xn),其分布函数是指F(x1,x2,…,xn) =P{X1£x1,X2£x2,…,Xn£xn},其中x1,x2,…,xn,为任意实数.
答案
设近似值x1,x2满足?(x1)=0.05,?(x2)=0.005,那么?(x1x2)=( ) .
答案
对于代数系统和, 若存在一个映射f:X→Y,使得对任意x1, x2∈X,有:f(x1*x2)=f(x1)⊙f(x2),f(x1°x2)=f(x1)◎f(x2), 则称f是从到的同态映射,称与同态。
答案
非线性模型中,当其他自变量保持不变,X1?变化△X1,因变量的期望值的变化量为:
答案
热门试题
若x1(t)傅立叶变换为X1(f),若x2(t)傅立叶变换为X2(f),则X1(f)*X2(f)的逆傅立叶变换为?(*代表卷积)
设F(x)是随机变量X的分布函数,则对()随机变量X,有P{x1 < X < x2}=F(x1) – F(x2)
设X1,X2,Y均为随机变量,已知Cov(X1,Y)=-1,Cov(X2,Y)=3,则Cov(X1+2X2, Y)=________.
设 x1,x2,xn为样本观测值,经计算知nx 2 =64,
映射f:A→B,若A中任意两个不同元素x1≠x2有f(x1)≠f(x2),则f是()
映射f:A→B,若A中任意两个不同元素x1≠x2有f(x1)≠f(x2),则f是
如果X的分布函数为F(x), 则对任意实数x1 < x2 ,有P{ x1 < x2 }=F(x2) – F(x1)()
试证明:在二元线性回归模型Y=β1+β2X2+β3X3+u中,当X2和X3相互独立时,对斜率系数β2和β3的OLS估计值。等于Y分对X2和X3作简单线性回归时斜率系数的OLS估计值。
在二元线性回归模型中,X1的系数表示_____
若函数f(x)对任意实数x1、x2均满足关系式f(x1+x2)=f(x1)f(x2)。且f′(0)=2,则必有( )
中国大学MOOC: 如果X的分布函数为F(x), 则对任意实数x1 < x2 ,有P{ x1 < X< x2 }=F(x2) – F(x1).
设X1、X2是随机变量,其数学期望、方差都存在,C是常数,下列命题中: (1) E(CX1+b)=CE(X1)+b (2) E(X1+X2)=E(X1)+E(X2) (3) D(CX1+b)=C2D(X1)+b (4) D(X1+X2)=D(X1)+D(X2) 正确的有( )
若函数f(x)在区间(a,b)内可导,x1和x2是区间(a,b)内任意两点(x1<x2),则至少存在一点ξ,使( )
设f(x)在(一∞,+∞)内有定义,且存在常数k与α>1,使|f(x1)-f(x2)|≤k|x1-x2|α对任意x1、x2成立.证明:f(x)=c (-∞
设f(x)在(-∞,+∞)内有定义,且存在常数k与α>1,使|f(x1)-f(x2)|≤k|x1-x2|α对任意x1、x2成立。证明:f(x)=c(-∞<x<+∞,c为常数)。
若x1,x2都是某一线性规划问题的最优解,则x=λ1×1+ λ2×2也是该线性规划问题的最优解,其中λ1、λ2满足()
已知A(x1,y1) , B(x2,y2)且x1≠x2,则直线AB的斜率为()
响应变量Y与两个自变量(原始数据)X1及X2建立的回归方程为:Y=2.1X1+2.3X2,由此方程可以得到结论是()
若X1,X2,X3两两不相关,且D(X1)=1(i=1,2,3),则D(X1+X2+X3)=____.
设随机变量X1和X2都服从[0,2]上的均匀分布,则E(X1+X2)=()。



 使用微信扫一扫登录
使用微信扫一扫登录