若函数f(x)在(a,b)内单调递增,且在(a,b)内可导,则必有f’(x)>0.
查看答案
相关试题
换一换


若函数f(x)在(a,b)内单调递增,且在(a,b)内可导,则必有f’(x)>0.
答案
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调。()
答案
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调()
A.正确 B.错误
答案
下列函数中,既是偶函数又在(0,+∞)内单调递增的是()
A.y=-ln|x| B.y=e|x| C.y=x3+x D.y=cosx
答案
若函数f(x)在(a,b)内二阶可导,且,则在(a,b)内的函数/ananas/latex/p/267640
答案
下列函数在其定义域内单调递增的是()
A. B.
B.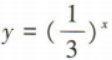 C.
C.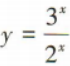 D.
D.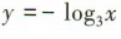
 B.
B.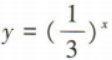 C.
C.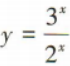 D.
D.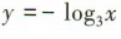
答案
下列函数在其定义域内单调递增的是()
A.y=lgx B.y=cosx C.y=2-x D.y=sinx
答案
下列函数中,在定义域内是单调递增函数的是()
A.y=2x B.y=1/x C.y=x2 D.y=tanx
答案
若函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则在(a,b)内满足()
A.必存在且只有一个 B.至少存在一个 C.不一定存在 D.不存在
答案
函数在区间上连续并且可导,若导数小于零,则函数在该区间上单调减少
答案
热门试题
函数在区间上连续并且可导,若导数为零,则函数在该区间上单调增加
下列是在其定义域内为单调递增函数的是( )
若f(x)是闭区间[a,b]上单调递增的连续函数,且f(a)f(b)
已知函数f(x)是奇函数,且在区间[1,2]上单调递减,则f(x)在区间[-2,-1]上是单调递增函数。()
若偶函数f(x)在[1,5]上是单调递增,且最小值是1,则f(x)在[-5,-1]上()
若函数f(x)=x²+x在区间(a,1-2a)上单调递增,则a的取值范围为()
已知(x)在区间(-∞,+∞)内为单调减函数,且(x)>(1),则x的取值范围是().
已知f(x)在其定义域内为可导的偶函数,且f′(-3)=-7,则f′(3)=()
单调函数的导函数也是单调函数。
单调函数的导函数也是单调函数。
奇函数f(x)在闭区间[-1,1]上可导,且f′(x)≤M(M为正常数),则必有()《》()
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内( ).《》( )
如果函数 在 的某邻域内都有 ,则 在该邻域内单调增加。()
设函数f(t)连续,t∈[-a,a],f(t)>0,且则在[-a,a]内必有()
若f(x)是在(-l,l)(l>1)内的不恒为0的可导奇函数,则f′(x)( )。
设函数f(x)在[a,b]上连续,在(a,b)内可导,f′(x)>0.若f(a)·f(b)<0,则y=f(x)在
(a,b)内()
若函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则在(a,b)内满足f ′(x0)=0的点x0( )。
设函数f (x)在(a, b)内可微,且≠0,则f(x)在(a,b)内()
证明:若f(x)为可导的奇函数,则其导函数f′(x)为偶函数.
设函数f(x)在x=2的某邻域内可导,且f′(x)=ef(x),f(2)=1,则f‴(2)=____。



 使用微信扫一扫登录
使用微信扫一扫登录