x,cosx线性无关
查看答案
相关试题
换一换


如果二阶常系数非齐次线性微分方程y″+ay′+by=e-xcosx有一个特解y*=e-x(xcosx+xsinx),则( )。
A.a=-1,b=1 B.a=1,b=-1 C.a=2,b=1 D.a=2,b=2
答案
设常系数方程y″+by′+cy=0的两个线性无关的解为y1=e-2xcosx,y2=e-2xsinx,则b=____,c=____。
答案
设常系数方程y″+by′+cy=0的两个线性无关的解为y1=e^-2xcosx,y2=e^-2xsinx,则b=( ),c=( )。
A.3;2 B.2;3 C.5;4 D.4;5
答案
若向量组有部分向量线性无关,则全体向量线性无关.??????(????)
答案
已知α,β,γ线性无关,则下列向量组中一定线性无关的是()。
A.α+β+2γ,α-2β+γ,2α-β+3γ B.5α-3β+γ,2α+β-γ,3α-4β+2γ C.3α+2β+4γ,α-β+γ,5α+5β+7γ D.2α+5β-3γ,7α-β-γ,α-β-γ
答案
x,cosx线性无关
答案
以y1=ex,y2=e2xcosx为特解的最低阶数的常系数线性齐次方程为____。
答案
设向量组α1、α2、α3线性无关,则下列向量组中线性无关的是( ).
A.α1+α2,α2+α3,α3-α1 B.α1+α2,α2+α3,α1+2α2+α3 C.α1+2α2,2α2+3α3,3α3+α1 D.α1+α2+α3,2α1-3α2+22α3,3α1+5α2-5α3
答案
∫xcosx2dx=
A.-2sinx2+C B.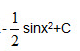 C.2sinx2+C D.
C.2sinx2+C D.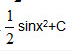
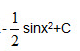 C.2sinx2+C D.
C.2sinx2+C D.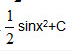
答案
若向量组α、β、γ线性无关,α、β,δ线性相关,则( ).
A.α必可由β、γ、δ线性表示 B.β必可由α、γ、δ线性表示 C.δ可由α、β、γ线性表示 D.δ必不可由α、β、γ线性表示
答案
热门试题
若向量组α,β,γ线性无关α,β,δ线性相关,则()
若向量组α,β,γ线性无关,α,β,σ线性相关,则( )。
设α1,α2,α3线性无关,证明α1+α2,α2+α3,α1+α3线性无关。
以y1=e^x,y2=e^2xcosx为特解的最低阶数的常系数线性齐次方程为( )。
函数y=xcosx+sinx是
凡是线性无关的方程一定有多余的方程,删掉这些多余的方程后,线性无关就变成了线性相关()
金属的线性电阻与()无关。
凡是线性无关的方程一定有多余的方程,删掉多余的方程后线性无关的方程就变成了线性相关()
线性分组码的监督矩阵各行是线性无关的()
金属导体的线性电阻于无关()
R上连续函数构成的线性空间中, sinx, cosx 线性无关
若A是m×n矩阵,且m≠n,则当A的列向量组线性无关时,A的行向量组也线性无关()
若A是m×n矩阵,且m≠n,则当A的列向量组线性无关时,A的行向量组也线性无关
下列结论正确的是: 若向量组A中有一部分向量线性无关,则向量组A线性无关|若向量组A线性无关,则A中任意一部分向量也线性无关|若向量组A线性相关,则A中任意一部分向量也线性相关|若向量组A线性相关,则A中每一向量都可由其余向量线性表示
对于光纤传输特性与()无关,称为线性。
线性无关的向量组是正交的
向量α(→)线性无关的充要条件是____。
线性电阻与所加、流过的电流无关()
对于光纤传输特性与()无关,称为线性
线性电阻元件与非线性电阻元件特性与元件电压或电流无关。()



 使用微信扫一扫登录
使用微信扫一扫登录