sin 120°=(),cos 150°=(),tan 300°=().
查看答案
相关试题
换一换


sin 120°=(),cos 150°=(),tan 300°=().
答案
已知tanα=-3,则cos²α-sin²α=()
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
若角α,β都是锐角,以下结论:
①若α<β,则sinα<sinβ;②若α<β,则cosα<cosβ;③若α<β,则tanα<tanβ;④若α+β=90°,则sinα=cosβ.其中正确的是( )
A.①② B.①②③ C.①③④ D.①②③④
答案
sinθ·cosθ·tanθ<0,则θ属于集合()。
A.{θ|<0<π} B.{θ|<0<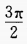 } C.Ø D.{θ|-
} C.Ø D.{θ|-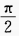 <θ<0}
<θ<0}
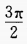 } C.Ø D.{θ|-
} C.Ø D.{θ|-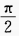 <θ<0}
<θ<0} 答案
已知tanα+sinα=m,tanα-sinα=n(m+n≠0),则cosα的值是()。
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
已知tanα=-1/2,则sin²α+ 2sinαcosα- 3cos²α的值是( )
A.-7/5 B.-9/5 C.3 D.-3
答案
sin 2·cos 3·tan 4的值().
A.小于0 B.大于0 C.等于0 D.不确定
答案
已知tanαsinα<0且sinαcosα>0,则α所在象限为( )
A.一 B.二 C.三 D.四
答案
sin180°-2cos0°-tan0°=
答案
教学课上,小明在学会了公式 sin(α+β)=sinaαcosβ+cosβsianα后,错误地认为tan(α+β)=tanαcotβ+cotαtanβ,这是一种()
A.正迁移 B.负迁移 C.顺向迁移 D.逆向迁移
答案
热门试题
若6sinαcosα=1,则tanα的值等于______。
已知sinα=3cosα,那么tan2α的值为()
函数SIN、COS、ASIN、ACOS、TAN和ATAN的角度单位是度
设向量a=(2,3sinθ),b=(4,cosθ),若a//b,则tanθ=()
已知角α终边上一点P(3,-4),则sinα+cosα-tanα=()。
sin245°﹣3tan230°+4cos260°的值是()
设tan α,tan β是方程x2+6x+7=0的两根,求证:sin(α+β)=cos(α+β).
已知sinθ+cosθ=m,tanθ+cotθ=n,则m与n的大小关系为()。
已知sinθ+cosθ=m,tanθ+cotθ=n,则m与n的大小关系为( )
已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
已知tan2θ=2tan2ψ+1,求cos2θ+sin2ψ的值。
Raptor中SIN(X)、COS(X)和TAN(X)函数的参数X的单位是( )。
当x趋于0时,(tan(6x)-cos(x)+1)/sin(3x)=()。
sin(α+β)cosβ-cos(α+β)sinβ=()
已知sinα-cosα=a,计算sinαcosα=()。
设f'(sin2x)=cos2x+tan2x,求f(x).
已知α的终边经过点P(3m,-4m),若m>0,则sinα =______,cosα =______,tanα=______.
设f′(sin2x)=cos2x+tan2x,当0<x<1时,求f(x)。
(sinα+sinβ)2+(cosα+cosβ)2=()。
cos12°cos98°-sin12°sin98°=()。



 使用微信扫一扫登录
使用微信扫一扫登录