z=x2+y2上原点为()。
查看答案
相关试题
换一换


z=x2+y2上原点为()。
答案
曲线y=y(x)经过原点且在原点处的切线与直线2x+y=6平行,而y=y(x)满足方程y″-2y′+5y=0,则此曲线的方程为____。
答案
原点到平面2x+y+4z=2的距离d=().
答案
圆x2+y2-6x+4y=0上到原点距离最远的点是( ).
A.(-3,2) B.(3.-2) C.(6.4) D.(-6,4) E.(6,-4)
答案
由曲线(x2+y2)2=a2(x2-y2)围成的均匀薄板(μ=1)对坐标原点的转动惯量为____。
答案
抛物线y=x2的顶点是原点。()
答案
曲线y=k(x2-3)2在拐点处的法线通过原点,则k=____。
答案
已知曲线y=y(x)经过原点,且在原点的切线平行于直线2x-y-5=0,而y(x)满足y″-6y′+9y=e3x,则y(x)等于( )。
A.sin2x B.x2e2x/2+sin2x C.x(x+4)e3x/2 D.(x2cosx+sin2x)e3x
答案
在数轴上原点以及原点右边的点表示的数是()
A.正数 B.负数 C.零和正数 D.零和负数
答案
已知曲线y=y(x)经过原点,且在原点处的切线平行于直线2x-y+5=0,而y(x)满足微分方程
y”-6y'+9y=0,则此曲线方程为y=()
A.sin2x B.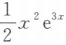 C.2xe3x D.2e3x
C.2xe3x D.2e3x
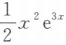 C.2xe3x D.2e3x
C.2xe3x D.2e3x 答案
热门试题
设圆C:x2+y2-6x-8y+9=0,则圆心到原点的距离为()。
设曲线积分∮L2[xφ(y)+ψ(y)]dx+[x2ψ(y)+2xy2-2xφ(y)]dy=0,其中L为任意一条平面曲线。求: (1)可微函数φ(y)、ψ(y)。已知φ(0)=-2,ψ(0)=1。 (2)求沿L从原点(0,0)到点M(π,π/2)的曲线积分。
设圆x2+y2+4x-8y+4=0的圆心与坐标原点问的距离为d,则 ( )
方程x2+y2=9表示圆心在原点,半径为3的一个圆。()
从原点向椭球面x2/a2+y2/b2+z2/c2=1的切平面作垂线,求垂足的轨迹方程。
设圆(x+2)2+(y-4)2=16的圆心与坐标原点间的距离为d,则()。
过坐标原点且与直线x-1/3=y+1/2=z-3/-2垂直的平面方程为()。
过坐标原点且与直线x-1/3=y+1/2=z-3/-2垂直的平面方程为_______
质点在y轴上运动,运动方程为y=4t2-2t3,则质点返回原点时的速度和加速度分别为[ ]()
求曲线y=e-x上通过原点的切线方程及与直线x+y=2垂直的法线方程.
两列波的表达式分别为y1=cos2Avtx(/)和y2=cos2Avtx(/),两波叠加后在坐标原点x=0处的振幅为()
已知原点是抛物线y=(m1)x2的最高点,则m()
过坐标原点且与平面2x-y+z+1=0平行的平面方程为______.
已知原点是抛物线y=(m1)x2的最高点,则m()
过原点且与平面2x-y+3z+5=0平行的平面方程为______.
过坐标原点且与平面2x-y+z+1=0平行的平行方程为()。
过原点且与平面2x-y+3z+5=0平行的平面方程为______。
过坐标原点且与平面2x-y+z+1=0平行的平面方程为______。
已知原点O(0,0),则点O到直线x+y+2=0的距离等于______
已知点A(x,5)关于点C(1,y)对称的点B(-2,-3),则点P(x,y)到原点的距离是()



 使用微信扫一扫登录
使用微信扫一扫登录