设平面区域D={(x,y)|x/2≤y≤1/(1+x^2),0≤x≤1},则D绕y周旋转所成旋转体体积为
查看答案
相关试题
换一换


设平面区域D={(x,y)|x/2≤y≤1/(1+x^2),0≤x≤1},则D绕y周旋转所成旋转体体积为
答案
设区域D={(x,y)|10≤y≤x2,0≤x≤1},则D绕x轴旋转一周所得旋转体的体积为
A.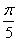 B.
B. C.
C.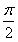 D.π
D.π
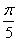 B.
B. C.
C.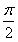 D.π
D.π 答案
设区域D={(x,y)|x2+y2≤1},D1={(x,y)|x2+y2≤1,x≥0,y≥0),则()
A.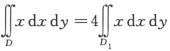 B.
B. C.
C.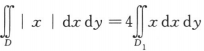 D.
D.
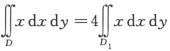 B.
B. C.
C.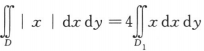 D.
D.
答案
设X,Y相互独立,且D(X)=D(Y)=1,则D(2X-Y)=
答案
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·①求平面图形的面积;②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.
答案
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3-1所示)。①求平面图形的面积;②求平面图形D绕x轴旋转一周所成旋转体的体积Vx。
答案
设X,Y的方差为D(X)=2,D(Y)=3,则D(X-Y)=-1()
答案
设A>0,D是由曲线段y=Asinx(0≤x≤π/2)及直线y=0,x=π/2所围成的平面区域,V1,V2分别是D绕x轴与y轴旋转所成旋转体的体积,若V1=V2,求A的值。
答案
设X、Y相互独立,且E(X)=0,E(Y)=1,D(X)=1,D(Y)=4,则E(X2Y2)=____。
答案
设D是由曲线x=1-y2与x轴、y轴,在第一象限围成的有界区域.求:(1)D的面积S;(2)D绕x轴旋转所得旋转体的体积V.
答案
热门试题
设E(X)=1,E(Y)=2,D(X)=1,D(Y)=4,ρXY=0.6,则E(2X-Y+1)2=____.
设E(X)=1,E(Y)=2,D(X)=1,D(Y)=4,ρXY=0.6,则E(2X-Y+1)2=( )。
设曲线x=√y、y=2及x=0所围成的平面图形为D.(1)求平面图形D的面积S。(2)求平面图形D绕y轴旋转一周所生成旋转体的体积Vy。
设X与Y相互独立,D(X)=1, D(Y)=2, 则 D(3X-2Y+1)的值为
已知曲线x=y+ey,直线x=y,y=1,y=2围成一平面图形D,求平面图形D绕y轴旋转一周所得的旋转体的体积Vy.
设D为曲线y=x2与直线y=x所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.
设D为曲线Y=X2与直线Y=X所围成的有界平面图形,求绕X轴旋转一周形成的面积V
设D为由曲线y=x2,y=0,x=2所围成的图形.
(1)求D的面积;
(2)求D绕x轴旋转一周所得旋转体的体积.
设D是由曲线x=1-y2与x轴、y轴,在第一象限围成的有界区域.求:(1)D的面积S;(2)D绕r轴旋转所得旋转体的体积V.
已知曲线y=x3(x≥0),直线x+y=2以及y轴围成一平面图形D,求平面图形D绕y轴旋转一周所得旋转体的体积.
中国大学MOOC: 设平面区域D由曲线 y = 1/x及直线 y = 0, x = 1, x = e2所围成,二维随机变量(X,Y)在区域D上服从均匀分布,则(X,Y)关于X的边缘概率密度在x = 2处的值为( ).
设x2+xy+y3=1,则(d2y/dx2)|x=1=____。
设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4,x≥0,y≥0,其面密度u(x,y)=2+y2,求该薄板的质量m.
设(X,Y )服从区域G:{0 £ x £ 2;0 £ y £ 2}上的均匀分布,则P{| X – Y | £ 1}=()
由曲线y=x2/2和直线x=1,x=2,y=-1围成的图形,绕直线y=-1旋转所得旋转体体积为:()
设随机变量(X,Y)在区域D={(x,y)| 0 < x < 1,0 < y < 1,}上服从均匀分布,则P{X < 0.5,Y <0.6} =()
曲线y=x^3,x=2,y=0所围成的平面图形绕y轴旋转所得旋转体的体积等于( )。
设X、Y相互独立,X~N(4,1),Y~N(1,4),Z=2X-Y,则D(Z)=()
设y'=2x,且x=1时,y=2,则y=().
设平面区域D由曲线xy=1及直线y=0,x=1,x=e2所围成,二维随机变量(X,Y)在区域D上服从于均匀分布,则(X,Y)关于X的边缘楠率密度函数在x=2处的值为____.



 使用微信扫一扫登录
使用微信扫一扫登录