F[x]中,若f(x)+g(x)=3,则f(0)+g(0)=()。
A. 0.0
B. 1.0
C. 2.0
D. 3.0
查看答案
相关试题
换一换


F[x]中,若f(x)+g(x)=3,则f(0)+g(0)=()。
A.0.0 B.1.0 C.2.0 D.3.0
答案
F[x]中,若f(x)+g(x)=3,则f(0)+g(0)=
答案
F[x]中,若f(x)+g(x)=3,则f(0)+g(0)=()
A.0 B.1 C.2 D.3
答案
设函数f(x,y)在点(0,0)附近有定义,且fx′(0,0)=3,fy′(0,0)=1,则( )。
A.dz|(0,0)=3dx+dy B.曲面z=f(x,y)在点(0,0,f(0,0))的法向量为(3,1,1) C.曲线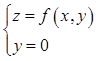 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线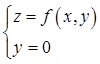 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1)
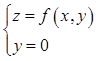 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线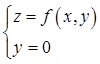 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1) 答案
设f(x)g(x)在x0处可导,且f(x0)=g(x0)=0,f′(x0)g′(x0)>0,f″(x0)、g″(x0)存在,则( )
A.x0不是f(x)g(x)的驻点 B.x0是f(x)g(x)的驻点,但不是它的极值点 C.x0是f(x)g(x)的驻点,且是它的极小值点 D.x0是f(x)g(x)的驻点,且是它的极大值点
答案
设f(x),g(x)∈F[x],若f(x)=0则有什么成立()
A.deg(f(x)g(x)) B.deg(f(x)g(x))>max{degf(x),degg(x)} C.deg(f(x)+g(x))>max{degf(x),degg(x)} D.deg(f(x)+g(x))=max{degf(x),degg(x)}
答案
设f(x),g(x)∈F[x],若f(x)=0则有什么成立()
A.deg(f(x)g(x)) B.deg(f(x)g(x))>max{degf(x),degg(x)} C.deg(f(x)+g(x))>max{degf(x),degg(x)} D.deg(f(x)+g(x))=max{degf(x),degg(x)}
答案
若f(-x)=f(x),且在(0,+∞)内f′(x)>0,f″(x)<0,则f(x)在(-∞,0)内( )。《》( )
A.f′(x)<0,f″(x)<0 B.f′(x)<0,f″(x)>0 C.f′(x)>0,f″(x)<0 D.f′(x)>0,f″(x)>0
答案
设f(x)g(x)均在[3,7]上连续,在(3,7)内可导,且g(x)≠0,f(3)=0,f(7)=0.证明:存在一点ξ∈(3,7),使得f′(ξ)g(ξ)-f(ξ)g′(ξ)=0.
答案
若f(-x)=-f(x)(-∞<x<+∞),且在(-∞,0)内f′(x)>0,f″(x)<0,则f(x)在(0,+∞)内是()
A.f′(x)>0,f″(x)<0 B.f′(x)<0,f″(x)>0 C.f′(x)>0,f″(x)>0 D.f′(x)<0,f″(x)<0
答案
热门试题
f(x)为偶函数,在(0,+∞)上为减函数,若f(1/2)>0>f(√3),则方程f(x)=0的根的个数是()。
若函数f(x)在点x0间断,g(x)在点x0连续,则f(z)g(x)在点x0:()
设函数f(x),g(x)均有二阶连续导数,满足f(0)>0,g(0)<0,f′(0)=g′(0)=0,则函数z=f(x)g(y)在点(0,0)处取得极小值的一个充分条件是( )。
设函数f(x)满足f”(x)-5f’(x)+6f(x)=0,若f(x0)>0,f'(x0)=0,则()。
设 函数f(x) 满足f"(x) — 5f" (x)+6f(x)=0若f(x0) > 0,f"(x0) == 0 则( )。
若函数f(x)在[0,1]上满足f"(x)>0,则f′(0),f′(1),f(1)-f(0)的大小顺序为().
若f(x)和g(x)在x=x0处都取得极小值,则函数F(x)=f(x)+g(x)在x=x0处( )
求证:设函数f(x),g(x)在点x=a可导,f(a)=g(a)=0且存在δ>0,使得当0<|x-a|<δ时,有|f(x)|≥|g(x)|,则|f′(a)|≥|g′(a)|。
设y=f(x)是方程y”-3y'+5y=0的一个解,若f'(x0)=0,且f(x0)>0,则函数f(x)()
若函数f(x)、g(x)满足下列条件:f′(x)=g(x),g′(x)=f(x),f(0)=0,g′(x)≠0。试求由曲线y=f(x)/g(x)与y=1、x=0、x=t(t>0)所围成的平面图形的面积。
设函数f(x,y)在点(0,0)的某邻域内有定义,且fx(0,0)=3,fy(0,0)=-1,则有( ).
设f(x),g(x)具有任意阶导数,且满足f″(x)+f′(x)g(x)+f(x)x=ex-1,f(0)=1,f′(0)=0。则( )。
若f(x)在区间[a,+∞)上二阶可导,且f(a)=A>0,f′(a)<0,f″(x)<0(x>a),则方程f(x)=0在(a,+∞)内( )。
若f(t)<----->F(s),Re【s】>s0,且有实常数t0>0,则()
已知函数y=f(x)对一切x满足xf″(x)+3x[f′(x)]^2=1-e-x,若f′(x0)=0(x0≠0),则( )。
对于分式f/g,当g≠0肘()当f=0,且g≠0时()
设函数f(x)满足f”(x)+2xf’(x)=3+ex,若f’(x0)=0,则()。
已知函数y=f(x)对一切x满足,若f’(x0)=0(x0≠0),则().
函数z=f(x,y)处可微分,且fx"(x0,y0)=0,fy"(x0,:y0)=0,则f (x,y)在P0(x0,y0)处有什么极值情况?
若函数f(z)在z_0不连续,则: (lim)┬(z→z_0 ) [f(z)-f(z_0)]=0|(lim)┬(z→z_0 ) [f(z)-f(z_0)]≠0|(lim)┬(z→z_0 ) f(z)=f(z_0)|(lim)┬(Δz→0) f(z_0+Δz)=f(z_0)



 使用微信扫一扫登录
使用微信扫一扫登录