设X=01100101B,将X依次左移一位,且最高位移至最低位,得到X1,再将X1和X之间的逐位逻辑“与”运算,则最后结果为_____。
A. 01000000B
B. 11001010B
C. 01100101B
D. 01000010B
查看答案
相关试题
换一换


设X=01100101B,将X依次左移一位,且最高位移至最低位,得到X1,再将X1和X之间的逐位逻辑“与”运算,则最后结果为_____。
A.01000000B B.11001010B C.01100101B D.01000010B
答案
设向量a=(2,1),b=(x,4),且a⊥b,则x=()
A.-1 B.1 C.-2 D.2
答案
应力放散时,应每隔(B)设一位移观测点观测钢轨位移量()
A.25~50m B.50~100m C.30~50m D.50~75m
答案
设X=-11/16,用二进制数表示时,符号取一位,尾数取四位,[X]原=(?????????),[X]补=(?????????)。
答案
设函数f(x),g(x)在[a,b]上连续,且在[a,b]区间积分∫f(x)dx=∫g(x)dx,则()
A.f(x)在[a,b]上恒等于g(x) B.在[a,b]上至少有一个使f(x)≡g(x)的子区间 C.在[a,b]上至少有一点x,使f(x)=g(x) D.在[a,b]上不一定存在x,使f(x)=g(x)
答案
设X服从b(n,p),且E(X)=2.4,D(X)=1.44 则p=( ),n=( )
答案
设函数f(x)在[a,b]上连续且f(x)>0,则
A.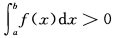 B.
B.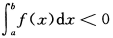 C.
C.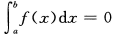 D.
D.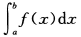 的符号无法确定
的符号无法确定
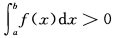 B.
B.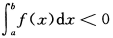 C.
C.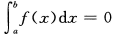 D.
D.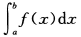 的符号无法确定
的符号无法确定 答案
设函数f(x)在[a,b]上连续且f(x)>0,则( )
A.见图A B.见图B C.见图C D.见图D E.见图E
答案
设函数f(x)在[a,b]上连续且f(x)>0,则()
A.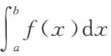 >0 B.
>0 B.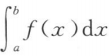 <0 C.
<0 C.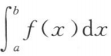 =0 D.
=0 D.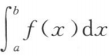 的符号无法确定
的符号无法确定
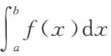 >0 B.
>0 B.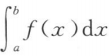 <0 C.
<0 C.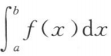 =0 D.
=0 D.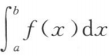 的符号无法确定
的符号无法确定 答案
63x25的积的最高位是百位()
答案
热门试题
设随机变量X~B(n,P),且E(X)=1.6,D(X)=1.28,则()。
设随机变量X~B(n,P),且E(X)=1.6,D(X)=1.28,则()。
设随机变量X~B(n,p),且E(X)=1.6,D(X)=1.28,则___()
设函数f (x)在(a, b)内可微,且≠0,则f(x)在(a,b)内()
设函数f(x)=x+b,且f(2)=3,则f(3)=______。
设函数f(x)=x+b,且f(2)=3,则f(3)=______。
设集合A={x∣x<1},B={x∣x<5},则A∪B={x∣x<5}。
设f(x)及g(x)在[a,b]上连续, f(x)g(x),且,在[a,b]上有( )/ananas/latex/p/1237/ananas/latex/p/106361
设函数f(x)对任意x均满足f(x+1)=af(x),且f′(0)=b,其中a,b为非零常数,则()
设函数,f(x)在[a,b]上连续,且F/(x)=f(x),有一点x0∈(a,b)使,f(x0)=0,且当a≤x≤x0时,f(x)>0;当x0<x≤b时,f(x)<0,则f(x)与x=a,x=b,x轴围成的平面图形的面积为()。
设X、Y相互独立且同服从分布B(n,p),设Z=X+Y,证明Z~B(2p,p).
设X、Y相互独立且同服从分布B(n,p),设Z=X+Y,证明Z~B(2n,p)。
设集合A={x|x≥1} ,B={x|-1
设函数f(x)=x3+x-1.(Ⅰ)求f(x)的单调区间;(Ⅱ)求出一个区间(a,b),使得f(x)在区间(a,b)存在零点,且b-a<0.5.
设函数f(x)与g(x)均在(a,b)可导,且满足f"(x)
设集合A={x|x²=1},B={x|x(x-1)=0},则A∪B=()
设函数?(x)在 R 上连续且可导。 (1)当?(x)=x2,且 g(x)=ex?(x)时,求证?(x)与 g(x)有共同驻点。(4 分) (2)当?(a)=f(b)=0(a<b)时,求证方程?′(x)+ ?(x)=0 在(a,b)内至少有一个实根。(6 分)
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )。
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有()
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。



 使用微信扫一扫登录
使用微信扫一扫登录