设A,B为同阶方阵, (1)若A,B相似,证明A,B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当A,B均为实对称矩阵时,证明(1)的逆命题成立
查看答案
相关试题
换一换


设AB为门阶方阵,若AB等价,则AB相似()
答案
设AB为门阶方阵,若AB等价,则AB相似
答案
设A、B都是n阶方阵,满足AB=A-B,请证明:AB=BA
答案
设A、B均为n阶方阵,A有n个互异的特征值,且AB=BA,证明:B相似于对角矩阵.
答案
若A,B为同阶方阵且均可逆,则AB亦可逆
答案
设A,B为同阶方阵, (1)若A,B相似,证明A,B 的特征多项式相等. (2)举一个二阶方阵的例子说明(1)的逆命题不成立. (3)当A,B均为实对称矩阵时,证明(1)的逆命题成立
答案
设A,B是n阶方阵,A≠0且AB=0,则( ).
A.| B.B=0; C.BA=O: D.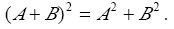
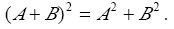
答案
设A,B是n阶方阵,A≠0且AB=0,则( ).
A.|B|=0或|A|=0: B.B=0; C.BA=O: D.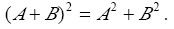
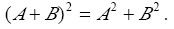
答案
设A、B都是满秩的n阶方阵,则r(AB)=____.
答案
设A、B都是满秩的n阶方阵,则r(AB)=( )。
A.1 B.2 C.n-1 D.n
答案
热门试题
设A为n阶方阵,若对任意n×m(m≥n)矩阵B都有AB=0,则A=____。
若三阶方阵A的特征多项式为f(λ)=λ3—7λ+6,则|A|=()。
设A、B都是4阶方阵且AB=0,则r(A)+r(B)____。
设A,B都是n阶对称阵,证明AB是对称阵的充要条件是AB=BA.
设A,B都是N阶对称矩阵,证明AB是对称矩阵的充分必要条件是.AB=BA
设 A 是方阵,如有矩阵关系式 AB=AC ,则必有( )
设A,B是n阶方阵,且AB=O.则下列等式成立的是().
设A,B是n阶方阵,且AB=0.则下列等式成立的是( ).
设A为3阶方阵,α(→)1,α(→)2,α(→)3是互不相同的3维列向量,且都不是方程组Ax(→)=0(→)的解,若B=(α(→)1,α(→)2,α(→)3)满足r(AB)<r(A),r(AB)<r(B),则r(AB)等于( )。
设A为3阶方阵,α1,α2,α3是互不相同的3维列向量,且都不是方程组AX=0的解,若B=(α1,α2,α3)满足r(AB)<r(A),r(AB)<r(B),则r(AB)等于( ).
设A、B为四阶方阵,r(A)=4,r(B)=3,则r[(AB)*]=( )。
设A与B都是n阶正交矩阵,证明AB也是正交矩阵.
设3阶矩阵A,B满足AB=A+B.证明A-E可逆.
设A是n级方阵,若存在矩阵B,使得AB=E,则A可逆()
已知A,B均为3阶方阵,|A|=2,|B|=-1,则|-2AB|=()。
设a>0,b>0,证明:ab+ba>1
设A,B,C均为n阶矩阵,若AB=C,且B可逆,则
设A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )。
设矩阵A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )
设矩阵A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )。



 使用微信扫一扫登录
使用微信扫一扫登录