当x→0时,2x+x2是x的( )
A. 等价无穷小
B. 较低阶无穷小
C. 较高阶无穷小
D. 同阶但不等价的无穷小
查看答案
相关试题
换一换


设f(x)是n次多项式:f(x)=a0+a1x+a2x2+…+anxn(an≠0),且f(x0)=f′(x0)=f″(x0)=…=f(m)(x0)=0,f(m+1)(x0)≠0(m<n-1)。试问x=x0是方程f(x)=0的多少重根?
答案
设函数f(x)可导,且曲线y=f(x)在点(x0,f(x0))处的切线与直线y=2-x垂直,则当Δx→0时,该函数在x=x0处的微分dy是( )。
A.与Δx同阶但不等价的无穷小 B.与Δx等价的无穷小 C.比Δx高阶的无穷小 D.比Δx低阶的无穷小
答案
设函数f(x)=x2-2x+4,曲线y=f(x)在(x0,f(x0))处的切线与直线y=x-1平行,则x0=
答案
如果函数f(x)当x→x0时极限存在,则函数f(x)在点x0处( )。
A.有定义 B.无定义 C.不一定有定义 D.连续
答案
设f(x)g(x)在x0处可导,且f(x0)=g(x0)=0,f′(x0)g′(x0)>0,f″(x0)、g″(x0)存在,则( )
A.x0不是f(x)g(x)的驻点 B.x0是f(x)g(x)的驻点,但不是它的极值点 C.x0是f(x)g(x)的驻点,且是它的极小值点 D.x0是f(x)g(x)的驻点,且是它的极大值点
答案
设y=f(x)满足关系式y″-2y′+4y=0,且f(x0)>0,f′(x0)=0,则f(x)在x0点处( )。
A.取得极大值 B.取得极小值 C.在x0点某邻域内单调增加 D.在x0点某邻域内单调减少
答案
设y=f(x)是y″-2y′+4y=0的一个解,若f(x0)>0且f′(x0)=0,则f(x)在点x0处( ).
A.取得极大值 B.某邻域内单调递增 C.某邻域内单调递减 D.取得极小值
答案
X0 在程序▕——▏▕——————[PLS M0]中,当X0接通时,M0接通
答案
当x→x0时,与x-x0。是等价无穷小的为()。
A.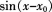 B.
B.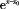 C.
C.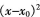 D.|n|x-x0|
D.|n|x-x0|
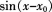 B.
B.答案
已知函数y=f(x)对一切x满足xf″(x)+3x[f′(x)]^2=1-e-x,若f′(x0)=0(x0≠0),则( )。
A.f(x0)是f(x)的极大值 B.f(x0)是f(x)的极小值 C.(x0,f(x0))是曲线y=f(x)的拐点 D.f(x0)不是f(x)的极值,(x0,f(x0))也不是曲线的拐点
答案
热门试题
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().
当x→0时,2x+x2是x的( )
当x→x0时,与x-x0叫。是等价无穷小的为()。
当x→x0时,与x-x0叫。是等价无穷小的为()。
y=f(x)是方程y″-2y′+4y=0的一个解,若f(x0)>0,f′(x0)=0,则函数f(x)( )。
当x→0时,x2是2x的( )
若取x0=2,y0为( )。
设f(x)在(-∞,+∞)可导,x0≠0,(x0,f(x0))是y=f(x)的拐点,则( )。
设曲线y=sinx(0≤x≤π/2),x轴及直线x=π/2所围成的平面图形为D,在区间(0,π/2)内求一点x0(0是下标),使直线x=x0 将D分为面积相等的两部分。
设f'(x0)=0,则x=x0
设函数θ(x)在(-∞,+∞)内连续,f(x)=cosθ(x),f′(x)=sinθ(x)。对θ(x0)≠nπ的x0,求θ′(x0)。
当x→0时,x2+Sinx是x的:()
当x→0时,x2+sinx是x的:
设f(x)=2x+3x-2,则当x→0时( ).
设f(x)=2
x-3
x=2,则当x→0时()。
(2011)如果f(x)在x0可导,g(x)在x0不可导,则f(x)g(x)在x0:()
设函数f(x)在定义域I上的导数大于零,若对任意x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)表达式。
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
已知f(-x)=-f(x)且f′(-x0)=m≠0,则f′(x0)=____。
已知f(-x)=-f(x)且f′(-x0)=m≠0,则f′(x0)=()



 使用微信扫一扫登录
使用微信扫一扫登录