2024年成考高起点每日一练《数学(理)》8月27日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:134
试卷答案:有
试卷介绍: 2024年成考高起点每日一练《数学(理)》8月27日专为备考2024年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 分别和两条异面直线AB、CD同时相交的两条直线AC、BD()。
A相交
B平行
C是异面直线
D垂直
-
2. 函数
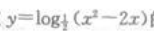 的定义域是()。
的定义域是()。A(-∞,0)∪[2,+∞)
B[0,2]
C(-∞,0)∪(2,+∞)
D(0,2)
-
3. 已知
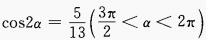 ,则tanα等于()。
,则tanα等于()。A
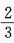
B
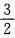
C
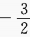
D
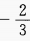
-
4. sinθ·cosθ·tanθ<0,则θ属于集合()。
A{θ|<0<π}
B{θ|<0<
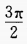 }
}CØ
D{θ|-
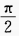 <θ<0}
<θ<0}
-
1. 已知设△ABC的三边长为a、b、C,2sin2A=3(sin2B+sin2C)且cos2A+3cosA+3cos(B-C)=1,求证:a:b:c=
 :1:1。
:1:1。
-
2. 已知lg2=a,lg3=b,求lg0.15关于a,b的表达式。
-
3. 计算 (1)tan5°+ cot5°- 2sec80°
(2)tan15°+cot15
(3)sin15°sin75°
-
4.
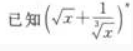 展开式的二项式系数之和比
展开式的二项式系数之和比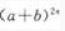 展开式的二项式系数之和小240。 求:(1)
展开式的二项式系数之和小240。 求:(1)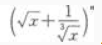 展开式的第3项;
展开式的第3项;
(2)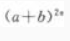 展开式的中间项。
展开式的中间项。
-
1. ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE、CE折起,使AE与BE重合如图
 ,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
-
2. 已知角α的终边过点P(-8m,-6cos60°)且cosα=-
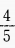 ,则m______。
,则m______。
相关试卷
相关题库