函数z=f(x,y)在P0(x0,y0)处可微分,且f′(x0,y0)=0,fy′(x0,y0)=0,则f(x,y)在P0(x0,y0)处有什么极值情况?()
A. 必有极大值
B. 必有极小值
C. 可能取得极值
D. 必无极值
查看答案
相关试题
换一换


函数z=f(x,y)处可微分,且fx"(x0,y0)=0,fy"(x0,:y0)=0,则f (x,y)在P0(x0,y0)处有什么极值情况?
A.必有极大值 B.必有极小值 C.可能取得极值 D.必无极值
答案
函数z=f(x,y)在P0(x0,y0)处可微分,且f′(x0,y0)=0,fy′(x0,y0)=0,则f(x,y)在P0(x0,y0)处有什么极值情况?()
A.必有极大值 B.必有极小值 C.可能取得极值 D.必无极值
答案
设函数f(x)可导,且曲线y=f(x)在点(x0,f(x0))处的切线与直线y=2-x垂直,则当Δx→0时,该函数在x=x0处的微分dy是( )。
A.与Δx同阶但不等价的无穷小 B.与Δx等价的无穷小 C.比Δx高阶的无穷小 D.比Δx低阶的无穷小
答案
设函数y=f(x)是微分方程y″+y′-2y=0的解,且在x=0处y(x)取得极值3,则y(x)=
答案
偏导数fx(x0,y0),fy(x0,y0)存在是函数z=f(x,y)在点(x0,y0)连续的()
A.充分条件 B.必要条件 C.充要条件 D.即非充分也非必要条件
答案
函数f(x,y)在点P0(x0,y0)处的一阶偏导数存在是该函数在此点可微分的( )。
A.必要条件 B.充分条件 C.充分必要条件 D.既非充分条件也非必要条件
答案
设y=f(x)是满足微分方程y″+y′-esinx=0的解,且f′(x0)=0,则f(x)在()
A.x0的某个邻域内单调增加 B.x0的某个邻域内单调减少 C.x0处取得极小值 D.x0处取得极大值
答案
设y=f(x)是微分方程y"-2y’+4y=0的一个解,又f(x0)>O,f’(x0)=0,则函数f(x)在点x0().
A.取得极大值 B.取得极小值 C.的某个邻域内单调增加 D.的某个邻域内单调减少
答案
设函数Z=f(x,y)可微,且(x0,y0)为其极值点,则əz/əx│(x0,y0)=______。
答案
设函数f(x,y)在点(0,0)附近有定义,且fx′(0,0)=3,fy′(0,0)=1,则( )。
A.dz|(0,0)=3dx+dy B.曲面z=f(x,y)在点(0,0,f(0,0))的法向量为(3,1,1) C.曲线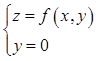 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线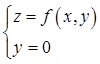 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1)
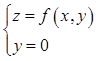 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线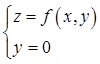 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1) 答案
热门试题
设y=f(x)满足关系式y″-2y′+4y=0,且f(x0)>0,f′(x0)=0,则f(x)在x0点处( )。
设函数y=y(x)是微分方程y″+y′-2y=0的解,且在x=0处取得极值3,则y(x)=
设y=f(x)是方程y”-3y'+5y=0的一个解,若f'(x0)=0,且f(x0)>0,则函数f(x)()
若z=f(x,y)在(x0,y0)处的两个一阶偏导数存在,则函数z=f(x,y)在(x0,y0)处可微
若z=f(x,y)在(x0,y0)处的两个一阶偏导数存在,则函数z=f(x,y)在(x0,y0)处可微
若z=f(x,y)在(x0,y0)处的两个一阶偏导数存在,则函数z=f(x,y)在(x0,y0)处可微()
设函数f(x,y)在点(0,0)的某邻域内有定义,且fx(0,0)=3,fy(0,0)=-1,则有( ).
设y=f(x)是y″-2y′+4y=0的一个解,若f(x0)>0且f′(x0)=0,则f(x)在点x0处( ).
已知二元函数f(x,y)在点(x0,y0)处偏导数存在,则fx(x0,y0)=0,fy(x0,y0)=0是函数f(x,y)在该点取得极值的()
设函数z=z(x,y)由方程F(y/x,z/x)=0确定,其中F为可微函数,且F2′≠0,则x·(?z/?x)+y·(?z/?y)=( )。
设f(x,y)与φ(x,y)均为可微函数,且φy′(x,y)≠0。已知(x0,y0)是f(x,y)在约束条件φ(x,y)=0下的一个极值点,下列选项正确的是( )。
已知函数f(x,y)满足fxy″=2(y+1)ex,fx′(x,0)=(x+1)ex,f(0,y)=y2+2y,求f(x,y)的极值。
y=f(x)是方程y″-2y′+4y=0的一个解,若f(x0)>0,f′(x0)=0,则函数f(x)( )。
设y=f(x)在点x=0处可导,且x=0为f(x)的极值点,则f’(0)=()。
设y=f(x)是微分方程y´´-2y´+4y=0的一个解,又f(xo)>0,f´(xo)=0,则函数f(x)在点xo()
考虑二元函数f(x,y)的下面4条性质:①f(x,y)在点(x0,y0)处连续;②f(x,y)在点(x0,y0)处的两个偏导数连续;③f(x,y)在点(x0,y0)处可微;④f(x,y)在点(x0,y0)处的两个偏导数存在。若用“P⇒Q”表示可由性质P推出Q,则有( )。
考虑二元函数f(x,y)的四条性质:
①f(x,y)在点(x0,y0)处连续;②f(x,y)的一阶偏导数在点x0,y0)处连续;③f(x,y)在点(x0,y0)处可微;④f(x,y)在点(x0,y0)处的一阶偏导数存在,
则下列关系正确的是()
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内( ).《》( )
函数y=f(x)在x0处可导,则在x0处的切线存在.
已知y0是微分方程y″+py′+qy=0的解,y1是微分方程y″+py′+qy=f(x)(f(x)≠0)的解,则下列函数中是微分方程y″+py′+qy=f(x)的解的是( )。



 使用微信扫一扫登录
使用微信扫一扫登录