设函数f(x)连续,由曲线y=f(x)在x轴围成的三块面积为均大于0),如图1-3-3所示,已知()
A. p-q
B. q-p
C. p+q
D. 2(p-q)
查看答案
相关试题
换一换


设函数f(x)连续,由曲线y=f(x)在x轴围成的三块面积为均大于0),如图1-3-3所示,已知()
A.p-q B.q-p C.p+q D.2(p-q)
答案
设函数f (x)连续,由曲线y=f (x)在x轴围成的三块面积为 ,如图1-3-3所示:()。
A.p-q B.q-p C.p+q D.2 (p-q)
答案
设函数f(x)在区间[a,b]连续,则曲线y=f(x)与直线x=a,x=b及x轴所围成的平面图形的面积为()
A.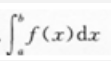 B.
B.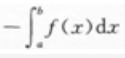 C.
C.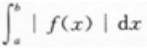 D.
D.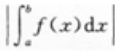
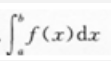 B.
B.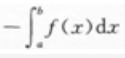 C.
C.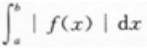 D.
D.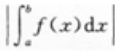
答案
设由连续曲线 及直线 所围成的曲边形绕 轴旋转一周得到的旋转体的表面积为 。
答案
设由连续曲线及直线所围成的曲边形绕轴旋转一周得到的旋转体的表面积为()
A.正确 B.错误
答案
设曲线y=cosx(0≤x≤π/2)与x轴、y轴所围成的图形面积被曲线y=asinx,y=bsinx(a>b>0)三等分,试确定a、b的值.
答案
设切线l是曲线y=x2+3在点(1,4)处的切线,求由该曲线,切线,及y轴围成的平面图形的面积S。
答案
设l是曲线y=x2+3在点(1,4)处的切线,求由该曲线,切线l及Y轴围成的平面图形的面积S.
答案
设l是曲线y=x2+3在点(1,4)处的切线,求由该曲线,切线l及Y轴围成的平面图形的面积S。
答案
曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为()
A.2 B.0 C.4
答案
热门试题
正态分布曲线从平均数到+∞区域与x轴围成的面积为()
曲线y=sinx在[-π,π]上与x轴所围成的图形的面积为( )。
求由曲线y=x2(x≥0),直线y=1及y轴围成的平面图形的面积。
由曲线y=x2,直线x=1及x轴所围成的平面有界图形的面积S=().
由曲线y=lnx,y轴与直线y=lna,y=lnb(b>a>0)所围成的平面图形的面积等于( )。
正态分布的密度曲线与x轴所围成的面积应等于1。
设D是由曲线x=1-y2与x轴、y轴,在第一象限围成的有界区域.求:(1)D的面积S;(2)D绕r轴旋转所得旋转体的体积V.
设D是由曲线x=1-y2与x轴、y轴,在第一象限围成的有界区域.求:(1)D的面积S;(2)D绕x轴旋转所得旋转体的体积V.
由曲线所围成的图形面积为/ananas/latex/p/716930
求由曲线y=x2(x≥0),直线y=1及y轴所围成的平面图形的面积.
曲线y=cosx在[0,2π]上与x轴所围成图形的面积是:
由曲线r=2cos所围成的图形的面积是
曲线y=-x3+x2+2x与x轴所围成的图形的面积A=____。
曲线y=1-x2与x轴所围成的平面图形的面积S=()·
曲线y=-x^3+x^2+2x与x轴所围成的图形的面积A=( )。
求一个正弦曲线与x轴所围成图形的面积(只计算一个周期的面积).
求一个正弦曲线与x轴所围成图形的面积.(只计算一个周期的面积).
设D为曲线Y=X2与直线Y=X所围成的有界平面图形,求绕X轴旋转一周形成的面积V
求曲线y=e-xsinx的x≥0的部分与x轴所围成的图形的面积.
曲线y=1-x2与x轴所围成的平面图形的面积S=()



 使用微信扫一扫登录
使用微信扫一扫登录