设A,B,C均为非零二阶矩阵,则下列各式正确的是()。
A. AB=BA
B. (AB)C=A(BC)
C. 若AB=0,则A=0或B=0
查看答案
相关试题
换一换


设A,B,C均为非零二阶矩阵,则下列各式正确的是()。
A.AB=BA B.(AB)C=A(BC) C.若AB=0,则A=0或B=0
答案
下列各式中正确是()。
A.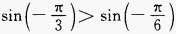 B.
B.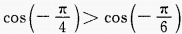 C.
C.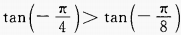 D.
D.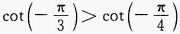
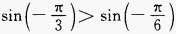 B.
B.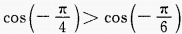 C.
C.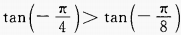 D.
D.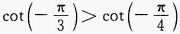
答案
设A是5×6矩阵,则()正确。
A.若A中所有5阶子式均为0,则秩RA.=4 B.B.若秩R=4,则A中5阶子式均为0 C.C.若秩R=4,则A中4阶子式均不为0 D.D.若A中存在不为0的4阶子式,则秩R=4
答案
设A是S×6矩阵,则()正确
A.若A中所有5阶子式均为0,则秩R(A)=4 B.若秩R(A)=4,则A中5阶子式均为0 C.若秩R(A)=4,则A中4阶子式均非0 D.若A中存在不为0的4阶子式,则秩尺(A)=4
答案
设A是5×6矩阵,则( )正确。
A.若A中所有5阶子式均为0,则秩R(A)=4 B.若秩R(A)=4,则A中5阶子式均为0 C.若秩R(A)=4,则A中4阶子式均不为0 D.若A中存在不为0的4阶子式,则秩R(A)=4
答案
设A.B均为n阶矩阵,则下列正确的为( )。
A.det(A+B)=detA+detB B.AB=BA C.det(AB)=det(AB) D.(A-B)2=A2-2AB+B2
答案
设A是m×n阶矩阵,则下列命题正确的是()
B.若mu003en,则方程组AX=b一定有唯一解 C.若r(A)=n,则方程组AX=b一定有唯一解 D.若r(A)=m,则方程组AX=b一定有解
答案
设A为可逆矩阵,则下列结论不正确的是()。
A.(A-1)-1=Abr/> B.|A-1|=|A|-1 C.(KA)-1=KA.-1(k≠0) D.(A")-1=(A-1)"
答案
设A是m×n阶矩阵,则下列命题正确的是()
B.若m>n,则方程组AX=b一定有唯一解 C.若r(A)=n,则方程组AX=b一定有唯一解 D.若r(A)=m,则方程组AX=b一定有解
答案
设A为可逆矩阵,则下列结论不正确的是()。
A.(A-1)-1=A B.|A-1|=|A|-1 C.(KA)-1=KA-1(k≠0) D.(A")-1=(A-1)"
答案
热门试题
设A是m×n阶矩阵,则下列命题正确的是().
设A.B均为n阶矩阵,则下列正确的为( )。
设A是实的反对称矩阵, 则下列命题正确的是
设A,B皆为n阶矩阵,则下列结论正确的是().
设X~N(0,1),则下列各式成立的有()
设x~N(0,1),则下列各式成立的有( )。
设N阶矩阵A与对角矩阵合同,则A是().
设函数f(x)=logax,且f(4)=2,则下列各式成立的是
设 A 为 n 阶矩阵,B 是经 A 若干次初等行变换得到的矩阵,则下列结论正确的是()
若a < b ,则下列各式正确的是( )。
中国大学MOOC: 设A是m行n列矩阵,R(A)=r,则下列正确的是
设A是m×n矩阵,B是n×m矩阵,则( )。
设A是M*N矩阵,B是N*M矩阵,则
设A是m×n矩阵,B是n×m矩阵,则( ).
设A,B均为n阶正定矩阵,则()是正定矩阵。
设A为n阶非零矩阵,E为n阶单位矩阵。若A3=O,则下列结论正确的是( )。
设A为n阶矩阵,A^2=A,则下列结论成立的是().
设A为n阶可逆矩阵,则(-A)的伴随矩阵(-A)n等于( )。
设矩阵A与B等价,则必有( )
设, 其中, 则矩阵A的秩等于()



 使用微信扫一扫登录
使用微信扫一扫登录