设z=f(u),而u=u(x,y)满足u=y+xφ(u)。若f和φ有连续导数,u存在偏导数,且xφ′(u)≠1,证明:∂z/∂x=φ(u)∂z/∂y。
查看答案
相关试题
换一换


设z=f(u),而u=u(x,y)满足u=y+xφ(u)。若f和φ有连续导数,u存在偏导数,且xφ′(u)≠1,证明:∂z/∂x=φ(u)∂z/∂y。
答案
设u=f(x+y,xz)有二阶连续偏导数,则∂2u/∂x∂z=( )。
A.f2′+xf11′+(x+z)f12″+xzf22″ B.xf12″+xzf22″ C.f2′+xf12″+xzf22″ D.xzf22″
答案
设u=f(x,y),v=F(x,y),其中f和F都是x和y的有一阶连续偏导数的函数。由此二式也确定了x和y都是u、v的有一阶连续偏导数的函数。证明:[(∂u/∂x)·(∂v/∂y)-(∂u/∂y)·(∂v/∂x)]·[(∂x/∂u)·(∂y/∂v)-(∂x/∂v)·(∂y/∂u)]=1。
答案
设二元函数F的两个偏导数F1′、F2′不同时为零,另一个二元函数u(x,y)满足F(∂u/∂x,∂u/∂y)=0(其中u(x,y)有二阶连续偏导数),证明:(∂2u/∂x2)·(∂2u/∂y2)=(∂2u/∂x∂y)2。
答案
设f(x)有连续导数,则下列关系式中正确的是:
A.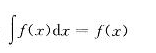 B.
B. C.
C.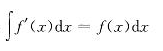 D.
D.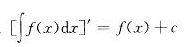
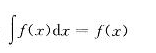 B.
B. C.
C.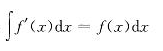 D.
D.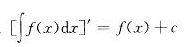
答案
(2013)设f(x)有连续导数,则下列关系式中正确的是:()
A.∫f(x)dx=f(x) B.[∫f(x)dx]′=f(x) C.∫f′(x)dx=f(x)dx D.[∫f(x)dx]′=f(x)=c
答案
(2013)设f(x)有连续导数,则下列关系式中正确的是:()
A.∫f(x)dx=f(x) B.[∫f(x)dx]′=f(x) C.∫f′(x)dx=f(x)dx D.[∫f(x)dx]′=f(x)=c
答案
设f(x)有连续的导数,则下列关系式中正确的是()
A.∫f(x)dx=f(x) B.(∫f(x)dx)′=f(x) C.∫f′(x)dx=f(x)dx D.(∫f(x)dx)′=f(x)+C
答案
设z=φ(x2-y2),其中φ有连续导数,则函数z满足( )。
A.x∂z/∂x+y∂z/∂y=0 B.x∂z/∂x-y∂z/∂y=0 C.y∂z/∂x+x∂z/∂y=0 D.y∂z/∂x-x∂z/∂y=0
答案
设u=f(x,y,z),φ(x2,ey,z)=0,y=sinx,其中f,φ都具有一阶连续偏导数,且∂φ/∂z≠0,求du/dx。
答案
热门试题
设偶函数f(x)具有二阶连续导数,且f″(0)≠0,则x=0( )。
设二元函数f(x,y)有连续偏导数,并且f(1,0)=f(0,1)。证明:在单位圆周上至少有两点满足方程y·∂f(x,y)/∂x=x·∂f(x,y)/∂y。
设函数z=F(π/2-arctanx,xy),其中F有二阶连续偏导数,求∂2z/∂x2。
设f具有一阶连续导数,且y=ef(2sinx),则y′=().
设z=f(x,xy)二阶偏导数连续,则∂2z/∂x∂y=____。
设z=f(x,y),φ(x,y)=0,其中f和φ对x、y具有二阶连续偏导数且φy′≠0,求z对x的二阶导数。
设y=y(x),z=z(x)是由方程z=xf(x+y)和F(x,y,z)=0所确定的函数,其中f和F分别具有一阶连续导数和一阶连续偏导数,求dz/dx。
设z=f(xy)/x+yφ(x+y),f和φ具有二阶连续导数,则∂2z/∂x∂y=____。
设z=f(x2-y2,cos(xy)),x=rcosθ,y=rsinθ,求∂z/∂r。其中f有一阶连续偏导数
设z=f(x2-y2,exy),其中f具有连续二阶偏导数,求∂z/∂x,∂z/∂y。
设函数f(x)在点x=O的某邻域内具有连续的二阶导数,且f′(0)=f″(0)=0,则( )。
设f(x),g(x)具有任意阶导数,且满足f″(x)+f′(x)g(x)+f(x)x=ex-1,f(0)=1,f′(0)=0。则( )。
(Ⅰ)设函数u(x),ν(x)可导,利用导数定义证明[u(x)ν(x)]’=u’(x)ν(x)+u(x)ν’(x); (Ⅱ)设函数u1(x),u2(x),…,un(x)可导,f(x)=u1(x)u2(x)…un(x),写出f(x)的求导公式.
设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为____。
设函数y=f(x)具有二阶导数,且f′(x)=f(π/2-x),则该函数满足的微分方程为( )。
设z=f(x+y,x/y,x),其中f具有连续二阶偏导数,求∂2z/(∂x∂y)。
设函数u=u(x,y)满足∂2u/∂x2-∂2u/∂y2=0及条件u(x,2x)=x,ux′(x,2x)=x2,u有二阶连续偏导数,则uxx″(x,2x)=( )。
设函数f(x)可导,则y=f{f[f(x)]}的导数为()
设函数在点的某一邻域内具有连续的偏导数,且,若,则方程在点的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数,它满足条件 ,并有
设z=f(xy)/x+yφ(x+y),f、φ具有二阶连续导数,则∂2z/∂x∂y=____。



 使用微信扫一扫登录
使用微信扫一扫登录