α1,...,αn为线性空间V(F)中的n个向量,下列哪个不成立?()
A. 若α1,
B. 若V(F)中任意一个向量可经向量组{α1,
C. 若α1,
D. 若秩{α1,
查看答案
相关试题
换一换


α1,...,αn为线性空间V(F)中的n个向量,下列哪个不成立?()
A.若α1, B.若V(F)中任意一个向量可经向量组{α1, C.若α1, D.若秩{α1,
答案
设向量组α1,…,αn为两两正交的非零向量组,证明:α1,…,αn线性无关,并举例说明逆命题不成立.
答案
设α1,α2,…,αn为n个线性无关的n维列向量,且与向量β正交.证明:向量β为零向量.
答案
设A为n阶可逆方阵,则( )不成立。
A.AT可逆 B.A2可逆 C.-2A可逆 D.A+E可逆
答案
设A为n阶可逆方阵,则( )不成立。
A.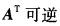 B.
B.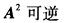 C.-2A可逆 D.A+E可逆
C.-2A可逆 D.A+E可逆
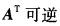 B.
B.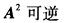 C.-2A可逆 D.A+E可逆
C.-2A可逆 D.A+E可逆 答案
n+1个n维向量一定线性相关
答案
n阶实对称矩阵A为正定矩阵,则下列不成立的是()。
A.所有k级子式为正(k=1,2,…,n) B.A的所有特征值非负 C.秩(A)=n
答案
n阶实对称矩阵A为正定矩阵,则下列不成立的是( )。
A.所有k级子式为正(k=1,2,…,n) B.A的所有特征值非负 C.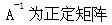 D.秩(A)=n
D.秩(A)=n
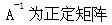 D.秩(A)=n
D.秩(A)=n 答案
设n阶方阵A=(α1,α2,…,αn),B=(β1,β2,…,βn),AB=(γ1,γ2,…,γn),记向量组(Ⅰ):α1,α2,…,αn,(Ⅱ):β1,β2,…,βn,(Ⅲ):γ1,γ2,…,γn,如果向量组(Ⅲ)线性相关,则( ).
A.向量组(Ⅰ)与(Ⅱ)都线性相关 B.向量组(Ⅰ)线性相关 C.向量组(Ⅱ)线性相关 D.向量组(Ⅰ)与(Ⅱ)中至少有一个线性相关
答案
n维向量组a1, a2, ××× , as线性无关, b为一n维向量, 则
答案
热门试题
设n维列向量组α1,α2,…,αm(m<n)线性无关,则n维列向量组β1,β2,…,βm线性无关的充分必要条件是( ).
以下哪个说法不成立:()
以下哪个说法不成立()
下列物体中重约为1N的是()
已知向量组α(→)1,α(→)2,…,α(→)n线性无关,讨论向量组α(→)1,α(→)1+α(→)2,α(→)1+α(→)2+α(→)3,…,α(→)1+α(→)2+…+α(→)n的线性相关性。
设n维向量组α1,α2,...,αm线性无关,则()。
任意n阶实称矩阵都存在n个线性无关的特征向量。()
n维向量组,α1,α2,…,αs(3≤s≤n)线性无关的充要条件是( ).
进行电平转换时,1N=()dB,1dB=()N
两个n维向量线性相关的充要条件是两个n维向量的各个分量对应成比例.
两个n维向量线性相关的充要条件是两个n维向量的各个分量对应成比例()
n维向量α1,α2,…,αs线性无关的充要条件是( ).
若A是m×n矩阵,且m≠n,则当A的列向量组线性无关时,A的行向量组也线性无关()
若A是m×n矩阵,且m≠n,则当A的列向量组线性无关时,A的行向量组也线性无关
下列各式中,不成立的是()。
进行电平转换时,1N=()dB, 1dB=()N。
下列物体重力约为1N的是()
使用齐次坐标可以将n维空间的一个点向量唯一的映射到n+1维空间中。()
使用齐次坐标可以将n维空间的一个点向量唯一的映射到n+1维空间中()
在强度的单位中,1N/mm=( )MPa



 使用微信扫一扫登录
使用微信扫一扫登录