过抛物线C:y2=4x的焦点作直线l,l交C于M,N两点,若线段MN中点的纵坐标为2,则|MN|=()
A. 10
B. 9
C. 8
D. 7
查看答案
相关试题
换一换


过抛物线C:y2=4x的焦点作直线l,l交C于M,N两点,若线段MN中点的纵坐标为2,则|MN|=()
A. 10 B.9 C.8 D.7
答案
过抛物线C:y2=4x的焦点作aT轴的垂线,交C于A,B两点,则|AB|=()。
A.2 B.4 C.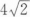 D.8
D.8
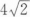 D.8
D.8 答案
过抛物线C:y2=4x的焦点作2轴的垂线,交C于A,B两点,则|AB|=()。
A.2 B.4 C.  D.8
D.8
 D.8
D.8 答案
已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线与抛物线C交于A,B两点,O为坐标原点,△AOB 的面积为 2.(1)求抛物线C的标准方程;
(2)若直线l与抛物线C交于P,Q两点,M(3,2)是线段PQ的中点,求直线l的方程.
(2)若直线l与抛物线C交于P,Q两点,M(3,2)是线段PQ的中点,求直线l的方程.
答案
过抛物线y2=4x的焦点,且斜率为2的直线l交抛物线于 A,B两点.(1)求直线l的方程;(2)求线段 AB 的长度.
答案
抛物线的顶点在原点,圆x2+y2=4x的圆心恰好为抛物线的焦点. (1)求抛物线的方程; (2)一条斜率为2,且过抛物线焦点的直线依次交抛物线和圆于A,B,C,D四点,求|AB|与|CD|的和.
答案
已知抛物线的顶点在原点,对称轴为y轴,焦点坐标F(0,1). (1)求抛物线的标准方程; (2)若过点A(0,m)且斜率为2的直线与该抛物线没有交点,求m的取值范围; (3)过焦点F且与x轴平行的直线与抛物线相交于P,Q两点,求以抛物线的焦点为圆心、PQ为直径的圆的方程.
答案
已知抛物线和双曲线都经过点M(1,2),它们在x轴上有共同的焦点,对称轴是坐标轴,抛物线的顶点为坐标原点. (1)求抛物线和双曲线标准方程; (2)已知动直线m过点P(3,0),交抛物线于A,B两点,记以线段AP为直径的圆为圆C,求证:存在垂直于x轴的直线l被圆C截得的弦长为定值,并求出直线l的方程.
答案
若直线x+y-3=0过抛物线y²=2px的焦点,则p=()
A. B.3 C.6 D.12
B.3 C.6 D.12
 B.3 C.6 D.12
B.3 C.6 D.12 答案
A,B是抛物线Y 2—8x上两点,且此抛物线的焦点段AB上,已知A,B两点的横坐标之和为10,则 ( )
A.18 B.14 C.12 D.10
答案
热门试题
A、B是抛物线y²=8x上两点,且此抛物线的焦点在线段AB上,已知A、B两点的横坐标之和为10,则|AB|=()
若抛物线y=ax2+bx+c(a≠0)经过A(1,4),B(3,4)两点,则抛物线的对称轴为直线()
A、B是抛物线y2=8x上两点,且此抛物线的焦点在线段AB上,已知A、B两点的横坐标之和为10,则|AB|=()。
已知抛物线 C的焦点F在x轴的正半轴上,顶点为坐标原点,若抛物线上一点M(2,m)满足|MF|=6,则抛物线C 的方程为()
已知焦点在y轴上的抛物线过 P(2,2).(1)求抛物线的标准方程;(2)已知直线l:y=x+b(b≠0)与抛物线交于点 A,B,若以 AB 为直径的圆过原点O,求直线l的方程.
已知过点(2,0)的直线l与抛物线 C:y2= 4x 交于 A,B 两点.
(1)若直线l的倾斜角为30°,求直线l与抛物线C准线的交点的坐标;
(2)求弦长|AB|的最小值,并求出此时直线l的方程.
过抛物线y2=4x的焦点,倾斜角为45°的直线方程为_______。
求过点(a,0)的直线方程,使该直线与抛物线 y=x2+1 相切。
已知抛物线的顶点在原点,对称轴为y轴,焦点F(0,1).(1)求抛物线的标准方程;(2)若过点A(0,m),且斜率为2的直线与该抛物线没有交点,求m的取值范围.
抛物线C:x²=4ay过点(-2,1),则C的准线方程为()
抛物线x2=4y上一点A的纵坐标为4,则点A与抛物线焦点的距离为( )
已知点P(2,m)在抛物线C:y²=8x上,则点P到C的焦点的距离为()
如图,在梯形A.B.C.D.中,,,A.C.交B.D.于O点,过O作A.B.的平行线交B.C.于E点,连结D.E交A.C.于F点,过F作A.B.的平行线交B.C.于G点,连结D.G交A.C.于M点,过M作A.B.的平行线交B.C.于N点,则线段MN的长为:
抛物线y2=8x上一点P到x轴距离为12,则点P到抛物线焦点F的距离为()
已知抛物线的方程为标准方程,焦点在x轴上,其上一点P(—3,m)到焦点距离为5,则抛物线方程为()。
抛物线C的顶点为坐标原点O,焦点在x轴上,直线l:x=1交C于点P,Q两点,且OP⊥OQ.已知点M(2,0),且⊙M与相切(1)求C,⊙M的方程;(2)设A1,A2,A3是C上的三个点,直线A1A2,A1A均与⊙M相切.判断直线A2A3与⊙M的位置关系,并说明理由.
设抛物线y=x2+2ax+b与x轴相交于A,B两点,点C坐标(0,2),若三角形ABC的面积等于6,则( ).
抛物线x²=6y的焦点位置在( )
抛物线y=5x²的焦点坐标为()
抛物线y=4x²的焦点坐标是()



 使用微信扫一扫登录
使用微信扫一扫登录