若f(u)可导,且y=f(ex),则dy=()
A. f"(ex)dx
B. f"(ex)exdx
C. f(ex)exdx
D. f"(ex)
查看答案
相关试题
换一换


若f(u)可导,且y=f(ex),则dy=()
A.f"(ex)dx B.f"(ex)exdx C.f(ex)exdx D.f"(ex)
答案
若f(u)可导,且y=f(ex),则dy=()
A.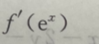 B.
B.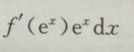 C.
C.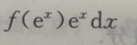 D.
D.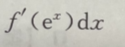
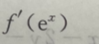 B.
B.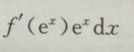 C.
C.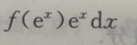 D.
D.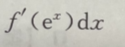
答案
若则dy/dx等于( )。
A.-tant B.tant C.-sint D.cott
答案
若则dy/dx等于()
A.- tant B.tant C.- sint D.cost
答案
若f(x)在[a,b]上连续,在(a,b)可导且f(a)=f(b),则()
A.至少存在一点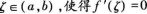 B.不一定存在一点
B.不一定存在一点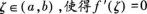 C.恰存在一点
C.恰存在一点 D.对任意的
D.对任意的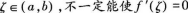
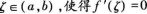 B.不一定存在一点
B.不一定存在一点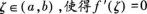 C.恰存在一点
C.恰存在一点 D.对任意的
D.对任意的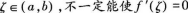
答案
若f(x)在[a,b]上连续,在(a,b)可导且f(a)=f(b),则( )。
A.至少存在一点ζ∈(a,b),使得f′(ζ)=0 B.一定不存在一点ζ∈(a,b),使得f′(ζ)=0 C.恰存在一点ζ∈(a,b),使得f′(ζ)=0 D.对任意的ζ∈(a,b),不一定能使f′(ζ)=0
答案
设y=f(x)为可导函数,则当△x→0时,△y-dy为△x的( )
A.高阶无穷小 B.等价无穷小 C.同阶但不等价无穷小 D.低阶无穷小
答案
若y=1+cosx,则dy=
A.(1+sinx)dx B.(1- sinx)dx C.sinxdx D.-sinxdx
答案
设单调函数y=y(x)二次可导,且满足微分方程d2y/dx2+(dy/dx)3=0,则其反函数x=x(y)满足方程d2x/dy2=1。
答案
f(x)可导,且f ′(x)>0,则()
A.F(0)是极大值 B.F(0)是极小值 C.F(0)不是极值,但(0,F(0))是曲线F(x)的拐点坐标 D.F(0)不是极值,(0,F(0))也不是曲线F(x)的拐点坐标
答案
热门试题
若函数f(x)在(a,b)内单调递增,且在(a,b)内可导,则必有f’(x)>0.
设函数f(x)在x=1处可导,且f"(1)=0,若f"(1)>0,则f(1)是()
若y=e2x,则dy=_________.
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调。()
若可导函数?(x)在区间I上单调,则其导函数?′(x)也单调()
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
设函数 f(x)在x=1处连续且可导,则( ).
设函数f(x)可导,且f(x)f"(x)>0,则
设函数f(x)可导,且f(x)f′(x)>0,则( )。
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
证明:若f(x)为可导的奇函数,则其导函数f′(x)为偶函数.
已知函数f(u)可微,且y=f(esecx),“①dy=tan2x·esecxf′(esecx)dx;②dy=secxtanxesecxf′(esecx)dx;③dy=secxtanxf′(esecx)dx;④dy=esecxf′(esecx)d(secx)”,4个结论中正确的是( )。
若f(x)在区间[a,+∞)上二阶可导,且f(a)=A>0,f′(a)<0,f″(x)<0(x>a),则方程f(x)=0在(a,+∞)内( )。
设y=f(lnx)ef(x),其中f可微,则dy=____。
设函数y=y(x)由方程y=f(x2+y2)+f(x+y)所确定,且y(0)=2,其中f是可导函数,f′(2)=1/2,f′(4)=1,则dy/dx|x=0=____。
下列命题正确的个数是()。(1)若f(x)是[a,b]上的连续函数,则f(x)在[a,b]上可导;(2)若函数f(x)在[a,b]上可导,则f(x)是[a,b]上的连续函数;(3)“函数f(x)在[a,b]上可导”是“函数f(x)在[a,b]上可微”的充要条件;(4)若f(x)是(a,b)上的连续函数,则f(x)在(a,b)上可积;(5)若函数f(x)在[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
下列命题正确的个数是()。 (1)若f(x)是[a,b]上的连续函数,则f(x)在[a,b]上可导; (2)若函数f(x)在[a,b]上可导,则f(x)是[a,b]上的连续函数; (3)函数f(x)在[a,b]上可导是函数f(x)在[a,b]上可微的充要条件; (4)若f(x)是(a,b)上的连续函数,则f(x) 在(a,b)上可积; (5)若函数f(x)在[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
设函数f(x)可导,且曲线y=f(x)在点(x0,f(x0))处的切线与直线y=2-x垂直,则当Δx→0时,该函数在x=x0处的微分dy是( )。
设y=f(x)二阶可导,且,f′(1)=0,f″(1)>0,则必有().
若函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则在(a,b)内满足()



 使用微信扫一扫登录
使用微信扫一扫登录