设f(x)是[-2,2]上的偶函数,且f'(-1)=3,则f'(1)=()
查看答案
相关试题
换一换


设f(x)是[-2,2]上的偶函数,且f′(-1)=3,则f′(1).
答案
设f(x)是[-2,2]上的偶函数,且f'(-1)=3,则f'(1)=()
答案
(2008)设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f′(x)>0,f″(x)>0则在(-∞,0)内必有:()
A.f′(x)>0,f″(x)>0 B.f′(x)0 C.f′(x)>0,f″(x)
答案
设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=()
A.-5 B.5 C.-10
答案
设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=( )
A.-5 B.5 C.-10 D.10
答案
设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=()。
A.-5 B.5 C.-10 D.10
答案
偶函数y= f(x)在(-∞,1)上是增函数,则f(x)在(1,+∞)上是()
A.增函数 B.减函数 C.先增后减 D.先减后增
答案
设f(x)是R上的偶函数,并且在[0,+∞)上单调递减,则f(-1),f(-3),f(5)的大小顺序是().
A.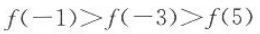 B.
B.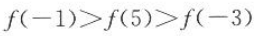 C.
C.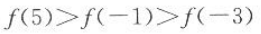 D.
D.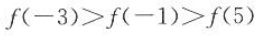
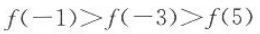 B.
B.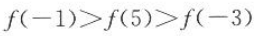 C.
C.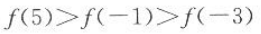 D.
D.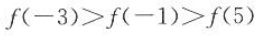
答案
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f(x)>0,f(x)>0,则在(-∞,0)内必有( )。
A.f(x)>0,f(x)>0 B. f(x) 0 B.f(x)>0,f(x)
答案
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f"(x)>0, f""(x)>0,则在(-∞,0)内必有:
A.f"(x)>0, f""(x)>0 B.f"(x)<0, f""(x)>0 C.f"(x)>0, f""(x)<0 D.f"(x)<0, f""(x)<0
答案
热门试题
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f"(x)>0,则在(-∞,0)内必有()。
f(x)偶函数,f(-1)=-3则f(1)=()
已知f(x)是偶函数且满足f(x+3)=f(x),f(1)=-1,则f(5)+f(11)等于()。
设f(x)为偶函数,若f(-2)=3,则f(2)=
设f(x)为偶函数,若f(-2)=3,则f(2)=
已知f(x)在R上是偶函数,若f(-2)=1,则f(2)=( )。
若二次函数f(x)是偶函数,且满足f(-1)=-1,f(0)=0,则f(x)的表达式是().
设F1(x?) 和F2(x?) 都是分布函数, 则F?(x?) = 0.3 F1(x?) + 0.7F1(x?) 也是一个分布函数.
已知偶函数f(x)在[0,+∞)上单调递减,且f(1)=-1,若f(2x-1)≥-1,则x的取值范围是()
若偶函数f(x)在[1,5]上是单调递增,且最小值是1,则f(x)在[-5,-1]上()
设f(x)是连续的偶函数,则其原函数F(x)一定是()
设有函数定义”int f1(void){ return 100 , 200 ; }”,设用函数f1()后
设偶函数f(x)在区间(-1,1)内具有二阶导数,且f″(0)=f′(0)+1,则f(0)为f(x)的一个极小值。
设偶函数f(x)在区间(-1,1)内具有二阶导数,且f″(0)=f′(0)+1,则f(0)为f(x)的一个极小值。
设偶函数f(x)在区间(-1,1)内具有二阶导数,且f″(0)=f′(0)+1,则f(0)为f(x)的一个极小值()
设偶函数f(x)具有二阶连续导数,且f″(0)≠0,则x=0( )。
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)在(-a,a)是连续的偶函数,且当0
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)是定义在[-a,a]上的任意函数,则下列答案中哪个函数不是偶函数?()



 使用微信扫一扫登录
使用微信扫一扫登录