若A、B为非零常数,C1、C2为任意常数,则微分方程y″+k2y=cosx的通解应具有形式( )。
A. C1coskx+C2sinkx+Asinx+Bcosx
B. C1coskx+C2sinkx+Axcosx
C. C1coskx+C2sinkx+Axsinx
D. C1coskx+C2sinkx+Axsinx+Bxcosx
查看答案
相关试题
换一换


若A、B为非零常数,C1、C2为任意常数,则微分方程y″+k2y=cosx的通解应具有形式( )。
A.C1coskx+C2sinkx+Asinx+Bcosx B.C1coskx+C2sinkx+Axcosx C.C1coskx+C2sinkx+Axsinx D.C1coskx+C2sinkx+Axsinx+Bxcosx
答案
微分方程的通解是()(C1、C2为任意常数)
A.lnx+C B.ln(x+C C.C2+ln D.C2-ln
答案
(2008)微分方程y″=(y′)2的通解是:(c1,c2为任意常数)()
A.lnx+c B.ln(x+C. C.c2+ln│x+c1│ D.c2-ln│x+c1│
答案
(2008)微分方程y″=(y′)2的通解是:(c1,c2为任意常数)()
A.lnxc B.ln(x C.c2ln│xc1│ D.c2-ln│xc1│
答案
微分方程yn=x+sinx的通解是(c1 ,c2为任意常数)()
A.(1/3)x3+ sinx+c1x+c2 B.(1/6)x3-sinx+c1x+c2 C.(1/2)x3-cosx+c1x-c2 D.(1/2)x3+sinx-c1x+c2
答案
微分方程y"-4y=6的通解是(c1,c2为任意常数):
A.c1e2x-c2e-2x+1 B.c1e2x+c2e-2x -1 C.e2x-e-2x +1 D.c1e2x+c2e-2x -2
答案
微分方程y″-4y=4的通解是( )。(c1,c2为任意常数)
A.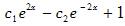 B.
B.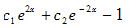 C.e2x-e-2x+1 D.c1e2x+c2e-2x-2
C.e2x-e-2x+1 D.c1e2x+c2e-2x-2
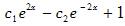 B.
B.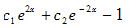 C.e2x-e-2x+1 D.c1e2x+c2e-2x-2
C.e2x-e-2x+1 D.c1e2x+c2e-2x-2 答案
微分方程y′′-4y=4的通解是(C1,C2为任意常数):
A.C1e2x-C2e-2x+1 B.C1e2x+C2e-2x-1 C.e2x-e-2x+1 D.C1e2x+C2e-2x-2
答案
在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。
A.y″+3y′-4y=0 B.y″-3y′-4y=0 C.y″+3y′+4y=0 D.y″+y′-4y=0
答案
设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为____。
答案
热门试题
设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为( )。
在下列微分方程中,以y=C1ex+C2cos2x+C3sin2x(C1,C2,C3为任意常数)为通解的是( )。
在下列微分方程中,以y=C1ex+C2cos2x+C3sin2x(C1,C2,C3为任意的常数)为通解的是( )。
微分y″=x+sinx方程的通解是( )。(c1,c2为任意常数)
若微分方程的解中含有独立的任意常数的个数与该微分方程的()相同,则该解叫作微分方程的通解.
已知微分方程y"+p(x)y = q(x)[q(x)≠0]有两个不同的特解y1(x), y2(x),C为任意常数,则该微分方程的通解是:
已知微分方程y"+p(x)y=q(x)[q(x)≠0]有两个不同的特解:y1(x),y2(x),则该微分方程的通解是:(c为任意常数)
微分方程ydx+(x-y)dy=0的通解是:(c为任意常数)
设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x),y2(x),C为任意常数,则该方程通解是()
(2012)已知微分方程y′+p+(x)y=q(x)[q(x)≠0]有两个不同的特解y1(x),y2(x),则该微分方程的通解是:(c为任意常数)()
微分方程的含有任意常数的解是该微分方程的通解。
微分方程的含有任意常数的解是该微分方程的通解()
函数:(:为任意常数)是微分方程y”-y’-2y=0的()
设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x),y2(x),C为任意常数,则该方程的通解是( )。
设非齐次线性微分方程y′+P(x)y=Q(x)有两个不同的解y1(x),y2(x),C为任意常数,则该方程的通解是( )。
设非齐次线性微分方程y´+P(x)y=Q(x)有两个不同的解析:y1(x)与y2(x),C为任意常数,则该方程的通解是()
设C是任意常数,则下列以y=Cex为解的二阶微分方程是()
设微分方程由通解y=(C1+C2x+x-1)e-x,求此微分方程。
函数y=C1e-x+C2(C1,C2为任意数)是微分方程y″-y′-2y=0的()
微分方程y″+y=xcos2x的一个特解应具有的形式是(其中A、B、C、D为常数):()



 使用微信扫一扫登录
使用微信扫一扫登录