阶矩阵 A 具有 n 个不同的特征值是 A 与对角矩阵相似的( )。
查看答案
相关试题
换一换


阶矩阵 A 具有 n 个不同的特征值是 A 与对角矩阵相似的( )。
答案
设A、B均为n阶方阵,A有n个互异的特征值,且AB=BA,证明:B相似于对角矩阵.
答案
n阶方阵A有n个不同的特征值是A与对角阵相似的( )
A.充分但非必要条件 B.必要但非充分条件 C.充分必要条件 D.既非充分条件也非必要条件
答案
n阶方阵A 有n个不同的特征值是A与对角阵相似的( )。
A.充分必要条件 B.充分而非必要条件 C.必要而非充分条件 D.既非充分也非必要条件
答案
已知n阶可逆矩阵A的特征值为λo,则矩阵的特征值是()
A.2/λo B.λo/2 C.1/2λo D.2λo
答案
已知A是n阶可逆矩阵,那么与A有相同特征值的矩阵是( )。
A.T B.2 C.-1 D.-E
答案
设N阶矩阵A与对角矩阵合同,则A是().
A.可逆矩阵 B.实对称矩阵 C.正定矩阵 D.正交矩阵
答案
中国大学MOOC: n阶方阵A与某对角矩阵相似,则( ).
答案
设A,B为N阶矩阵,且A,B的特征值相同,则().
A.A,B相似于同一个对角矩阵 B.存在正交阵Q,使得Q^TAQ=B C.r(A)=r(B) D.以上都不对
答案
若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则( )
A.A与B相似 B.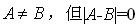 C.A=B D.A与B不一定相似,但|A|=|B|
C.A=B D.A与B不一定相似,但|A|=|B|
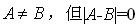 C.A=B D.A与B不一定相似,但|A|=|B|
C.A=B D.A与B不一定相似,但|A|=|B| 答案
热门试题
与n阶单位矩阵E相似的矩阵是
中国大学MOOC: n阶方阵A相似于对角矩阵的充要条件是A有n个( )。
若n阶矩阵A满足A2-A=2E,则A一定相似于对角矩阵.
下列命题错误的是: 属于不同特征值的特征向量线性无关|属于同一特征值的特征向量线性相关|特征值相同的矩阵不一定相似|相似矩阵必有相同的特征值
下列关于Jordan标准形描述正确的是( ): 不能是对角矩阵 可以是对角矩阵 对角元均是特征值 是上三角矩阵
相似矩阵必有相同的特征值. ( )
试证若n阶矩阵A满足A2-A=2E,则A一定相似于对角矩阵。
系数矩阵有3个不同的特征值。()
设A,B为n阶矩阵,且A与B相似,E为n阶单位矩阵,则
设A为m×n阶实矩阵,且r(A)=n.证明:A^TA的特征值全大于零.
设A是3阶实对称矩阵,Р是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值入的特征向量,则B的属于特征值A的特征向量是()
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知a是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:
(2009)设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:()
(2009)设A是3阶实对称矩阵,P是3阶可逆矩阵,B=P-1AP,已知α是A的属于特征值λ的特征向量,则B的属于特征值λ的特征向量是:()
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是( )。
设n阶矩阵A可逆,α是A的属于特征值λ的特征向量,则下列结论中不正确的是()。
设A、B都是n阶实对称矩阵,证明:存在正交矩阵Q,使Q-1AQ=B的充分必要条件是A与B有相同的特征值。
设3阶方阵A有特征值2,且已知|A|=5,则A的伴随矩阵必有特征值().



 使用微信扫一扫登录
使用微信扫一扫登录