设X~N(μ1,σ12),Y~N(μ2,σ22),X、Y相互独立,Z=X-Y,则Z的概率密度函数为fZ(z)=____。
查看答案
相关试题
换一换


设X1,X2,…,Xn相互独立且同服从分布B(1,p),Z=X1+X2+…+Xn,证明Z~B(n,p)。
答案
设z=xy,则dz=()
A.yxy-1dx+xyInxdy B.xy-1dx+ydy C.xy(dx+dy) D.xy(xdx+ydy)
答案
设z=xy,则dz=()。
答案
设X~N(μ1,σ12),Y~N(μ2,σ22),X、Y相互独立,Z=X-Y,则Z的概率密度函数为fZ(z)=____。
答案
设z=exy,则dz=()
答案
设z=exy,则dz=()。
A.exydx+exydy B.exdx+eydy C.yexydx+xexydy D.eydx+exdy
答案
设函数z=xy,则全微分dz_______.
答案
设随机变量X与Y相互独立,且X服从标准正态分布N(0,1),Y的概率分布为P{Y=0}=P{Y=1}=1/2记FZ(z)为随机变量Z=XY的分布函数,则函数FZ(z)的间断点个数为( )。
A.0 B.1 C.2 D.3
答案
设z=arctan[xy+sin(x+y)],则dz|(0,π)=
答案
设函数z=sin(xy),则下列结论正确的是().
A.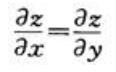 B.
B.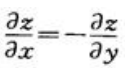 C.
C.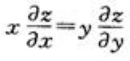 D.
D.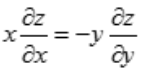
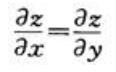 B.
B.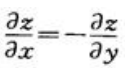 C.
C.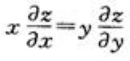 D.
D.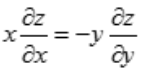
答案
热门试题
设z=f(x,xy)二阶偏导数连续,则∂2z/∂x∂y=____。
设z=f(xy,x/y)+g(y/x),其中f、g均可微,则∂z/∂x=____。
设二元函数z=xy,则点Po(0,0)()
设X、Y相互独立,X~N(4,1),Y~N(1,4),Z=2X-Y,则D(Z)=()
设f有二阶偏导数,z=f(xy),则∂2z/∂x∂y等于( )。
设事件A,B相互独立,A,B发生的概率分别为0.6,0.9,则A,B都不发生的概率为()。
设X、Y相互独立,X~E(λ),Y~E(μ),Z=min(X,Y),证明Z~E(λ+μ)。
设z=sin(xy)+cos2(xy),求dz.
设(X,Y)的联合概率密度为则数学期望E (XY)等于( )。
设(X,y)的联合概率密度为,则数学期望E(XY)等于()
设z=z (x, y)是由方程xz-xy+ln (xyz) =0所确定的可微函数,则z/y等于()
设随机事件A、B、C相互独立,则( )。
若随机变量X~N (3,9),Y~N (-1,4),且X与Y相互独立。设Z=X-Y,则Z~_____
设X、Y相互独立且同服从分布B(n,p),设Z=X+Y,证明Z~B(2p,p).
设X、Y相互独立且同服从分布B(n,p),设Z=X+Y,证明Z~B(2n,p)。
中国大学MOOC: 设随机变量X1, X2,…,Xn相互独立,Sn=X1+X2+…+Xn,则根据中心极限定理,当n充分大时,Sn近似服从正态分布,只要X1, X2,…,Xn().
设z=z (x,y)是由方程xz-xy+1n (xyz) =0所确定的可微函数,则 等于( )。
设z=f(xy)/x+yφ(x+y),f、φ具有二阶连续导数,则∂2z/∂x∂y=____。
设z=f(xy)/x+yφ(x+y),f和φ具有二阶连续导数,则∂2z/∂x∂y=____。
设z=sin(xy)+2x2+y,求dz.



 使用微信扫一扫登录
使用微信扫一扫登录