函数f(x,y)=sinx·cosy在点(0,1)处的梯度是()
A. {cos1,0}
B. -{cos1,0}
C. {0,cos1}
D. -{0,cos1}
查看答案
相关试题
换一换


函数f(x,y)=sinx·cosy在点(0,1)处的梯度是()
A.{cos1,0} B.-{cos1,0} C.{0,cos1} D.-{0,cos1}
答案
函数f(x,y)=arctan(x/y)在点(0,1)处的梯度等于( )。
A.i(→) B.-i(→) C.j(→) D.-j(→)
答案
由于函数极值点的必要条件是函数在这一点的梯度值的模为(),因此当迭代点的函数梯度的模已充分小时,则认为迭代可以终止。
答案
函数u=2xy-z2在点A(2,-1,1)处沿点A到点B(3,1,-1)方向的方向导数为(),在点A(2,-1,1)处的梯度为().
答案
函数在某点处存在极限,则该点处函数值一定存在()
答案
下列函数中,在点(0,0)处连续的函数是( )。
A.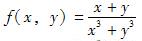 B.
B.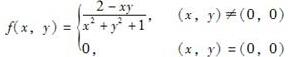 C.
C. D.
D.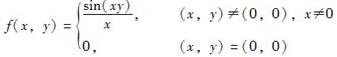
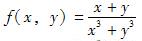 B.
B.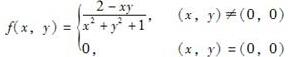 C.
C. D.
D.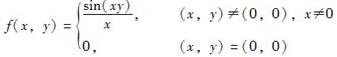
答案
函数在点x=0处( )。
A.不连续 B.连续但不可导 C.可导但导函数不连续 D.导函数连续
答案
设函数f(x)在点x=a处可导,则函数|f(x)|在点x=a处不可导的充分条件是( )
A.f(a)=0且f′(a)=0 B.f(a)=0且f′(a)≠0 C.f(a)>0且f′(a)> D.f(a)<0且f′(a)<
答案
函数y=f'(x)在点x0处可导是函数f(x)在点x0处连续的()。
A.充分条件 B.必要条件 C.充分必要条件 D.既非充分也非必要条件
答案
函数处有一阶偏导数是函数在该点连续的()
A.必要条件 B.充分条件 C.充分必要条件 D.既非充分又非必要条件
答案
热门试题
函数f (x, y) 在点处有一阶偏导数是函数在该点连续的( )。
函数f(x,y)在点处有一阶偏导数是函数在该点连续的()
函数的梯度方向就表示函数值下降最快的方向,梯度的反方向就是函数值增长最快的方向。()
设函数在点处存在偏导数
函数f (x,y)在点处的一阶偏导数存在是该函数在此点可微分的()。
函数z=f(x,y)在点(x,y)处的偏导数存在是函数在该点可微的()
函数在某点处的极限存在与在该点处有无定义有关
隐函数存在的前提是函数f(x,y)在某点P0处()
[ZJJK02-01-X]压力梯度是指压力的变化量()
函数f (x, y) 在点Po (xo, yo) 处有一阶偏导数是函数在该点连续的()
函数y=f(x)在点xo处的左、右极限存在且相等是函数在该点极限存在的( ).《》( )
设函数f(x)=丨x丨,则函数在点x=0处()
下列函数中,在点x=0处可导的是()
函数在点处是否可导?为什么?
中国大学MOOC: 二元函数梯度计算函数格式为()
函数f(x)在点x0处有定义,是f(x)在点x0处连续的()
已知下列命题:
命题A:函数f(x)在点x0处可导;
命题B:函数f(x)在点x0处可微;
命题C:函数f(z)在点x0处连续;
命题D:函数f(z)在点x0处极限存在;
命题E:函数f(工)在点x0处有定义.
试给出以上五个命题之间的相互推导关系.
函数f(x)在点x=a处的左右极限存在且相等,则它是函数在x=a处连续的
在点x=0处的导数等于零的函数是( )
在点x=0处的导数等于零的函数是()。



 使用微信扫一扫登录
使用微信扫一扫登录