设f(x)在区间[a,b]上连续,对区间内()两点x1,x2,有f((x1+x2)/2)≤1/2(Ψ(x)+x),则称在区间[a,b]上是凸的
查看答案
相关试题
换一换


设f(x)在区间[a,b]上连续,对区间内()两点x1,x2,有f((x1+x2)/2)≤1/2(Ψ(x)+x),则称在区间[a,b]上是凸的
答案
若函数f(x)在区间(a,b)内可导,x1和x2是区间(a,b)内任意两点(x1<x2),则至少存在一点ξ,使( )
A.f(b)-f(a)=f′(ξ)(b-a)(a<ξ<b) B.f(b)-f(x1)=f′(ξ)(b-x1)(x1<ξ<b) C.f(x2)-f(x1)=f′(ξ)(x2-x1)(x1<ξ<x2) D.f(x2)-f(a)=f′(ξ)(x2-a)(a<ξ<x2)
答案
设近似值x1,x2满足?(x1)=0.05,?(x2)=0.005,那么?(x1x2)=( ) .
答案
已知f(x)=x2+ax+b,则0≤f(x)≤1.(1)f(x)在区间[0,1]中有两个零点(2)f(x)在区间[1,2]中有两个零点
A.条件(1)充分,但条件(2)不充分 B.条件(2)充分,但条件(1)不充分 C.条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分 D.条件(1)充分,条件(2)也充分 E.条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案
y=fx在点x0连续,则y=fx在点x0必定可导()
答案
设(X,Y)~N(μ1,μ2,σ12,σ22,ρ),则随机变量X的边缘密度函数为fX(x)=____。
答案
设数X在区间(0,1)上随机的取值,当观察到X=x(0
答案
设数X在区间(0,1)上随机的取值,当观察到X=x(0<x<1)时,数Y在区间(x,1)上随机取值,则fY(y)=____。
答案
函数f(x)=(1-cos(x))/x2在什么区间连续()。
答案
函数:y=x2-2x-3的图像与直线y=x+1交于A,B两点,则|AB|=()。
A. B.4 C.
B.4 C. D.
D.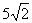
 B.4 C.
B.4 C. D.
D.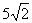
答案
热门试题
函数:y=x2-2x-3的图像与直线y=x+1交于A,B两点,则|AB|=()。
设函数f(x)在区间[0,2]上连续,在区间(0,2)内可导,且f(0)=f(2)=f(1)=2,证明:至少存在一点ξ∈(0,2),使得f′(ξ)=ξ.
设函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,且f(0)=0,f(1)=1/3,证明:存在ξ∈(0,1/2),η∈(1/2,1),使得f′(ξ)+f′(η)=ξ2+η2。
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上( )。
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
设数据x1,x2的绝对误差分别为0.025和0.006,那么两数的乘积x1x2的绝对误差为__()
函数f(x)=1/ln(x-1)的连续区间是()
设函数f(x)=x3+x-1.(Ⅰ)求f(x)的单调区间;(Ⅱ)求出一个区间(a,b),使得f(x)在区间(a,b)存在零点,且b-a<0.5.
设f'(x)在-闭区间[0,1]上连续,则曲线y=f(x)与直线x=0,x=1和y=0所围成的平面图形的面积等于()
设f(x,y,z)=exyz2,其中z=z(x,y)是由x+y+z+xyz=0确定的隐函数,则fx′(0,1,-1)=____。
设X是连续型随机变量,P{|X|≤1}=1。证明:对任意0<ε≤1,有P{|X|≥ε}≥E(X2)-ε2。
设f(x)在(a,b)内二阶可导,且f″(x)≥0,证明:对于(a,b)内任意两点x1、x2及0≤t≤1,有f[(1-t)x1+tx2]≤(1-t)f(x1)+tf(x2)。
若f″(x)不变号,且曲线y=f(x)在点(1,1)上的曲率圆为x2+y2=2,则函数f(x)在区间(1,2)内( )。
已知函数f(x)是奇函数,且在区间[1,2]上单调递减,则f(x)在区间[-2,-1]上是单调递增函数。()
函数f(x)=-x2+1在区间[-1,2]上的最小值为
设随机变量X的绝对值不大于1,P(X=-1)0.125,P(X=1)=0.25,在事件A={-1<X<1}出现的条件下,X在区间(-1,1)内的任意子区间上取值的条件概率与该子区间的长度成正比,求X的分布函数F(x).
设函数f(x)在闭区间[0,1]上可微,对于[0,1]上的每一个x,函数f(x)的值都在开区间(0,1)内,且f′(x)≠1,证明在(0,1)内有且仅有一个x,使得f(x)=x。
已知函数f(x)在区间[0,1]上连续,在区间(0,1)内可导,且f(0)=0,f(1)=1,证明:
(1)存在一点ξ∈(0,1),使得f(ξ)=1-ξ;
(2)存在两个不同的点η,ζ∈(0,1),使得f′(η)f′(ζ)=1.
设X是连续性随机变量,P{|X|≤1}=1.证明:对任意0<ε≤1,有P{|X|≥ε}≥E(X2)-ε2.
已知奇函数f(x)在区间[1,2]上的最小值为3,最大值为4,则f(x)在区间[-2,-1]上的()



 使用微信扫一扫登录
使用微信扫一扫登录