在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积
查看答案
相关试题
换一换


在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积。
答案
在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积
答案
已知△ABC中,A=60°,AB=AC=2,求:(1)BC;(2)△ABC的面积。
答案
在△ABC中,AB=2,BC=3,B=60°,BD为AC边上的高.求AC,BD.
答案
已知△ABC中,A=30°,AC=BC=1求(1)AB;(2)△ABC的面积.
答案
已知△ABC中,A=30°,AC=BC=1.求(Ⅰ)AB;(Ⅱ)△ABC的面积.
答案
已知△ABC中,A=30°,AC=BC=1.求(I)AB;(II)△ABC的面积
答案
在△ABC中,∠B=60°,AB=2,M是BC的中点,AM =2√3,则AC=_______,cos∠MAC=_______
答案
在△ABC中,AB=4,BC=6,∠ABC=60°,则AC=()。
A.128 B.76 C.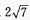 D.
D.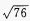
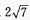 D.
D.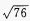
答案
在直角△ABC中,∠A=90°,AB=2,AC=3,则∠ABC的面积等于_____
答案
热门试题
在∆ABC中,∠ABC=600,AB=4,BC=6,则AC=()。
已知△ABC中,A=110°,AB=5,AC=6,求BC.(精确到0.01)
已知△ABC中,A=110°,AB=5,AC=6,求BC.(精确到0.01)
在△ABC中,AB=3,BC=5,AC=7,则cosB=()。
在△ABC中,B=120°,C=30°,BC=4,求△ABC的面积.
在△ABC中,已知AB=3,BC=5,AC=7,则cosB=______。
设A(1,2,3),B(-1,2,0),C(1,1,1)则AB(→)·BC(→)=____,AB(→)×BC(→)=____,△ABC的面积=____。
在△ABC中,若B=30°,BC=4,AB=5,则△ABC的面积为()
在△ABC中,内角A,B,C的对边分别为a,b,c,且a=3,b=2,A=60°.
(1)求sinB;
(2)求△ABC的面积
在△ABC中,AC=15,BC=10,B=60°,则sinA=()
在△ABC中,已知B=60°,b2=ac,那么△ABC是().
在△ABC中,A=30°,AC=20,AB=7,则△ABC的面积为()
在△ABC中,角A,B,C的对边分别为a,b,c,且a2-c2+b2=ab.
(1)求角C的大小;
(2)若a=b=3,求△ABC的面积.
已知∆ABC内,AB=2,BC=4,∠ABC=45°,BC在a内,且∆ABC所在平面与平面a成30°,则∆ABC在a内射影的面积是()
已知a,b,c分别是△ABC内角A,B,C的对边,且(b-c)2=a2-bc.
(1)求角A的大小;
(2)若a=3,sinC=2sinB,求△ABC的面积.
△ABC中,已知AC=12,∠A=30°,∠B=120°,则BC=()
设正整数a,b,c,满足a
设a、b、c皆为质数,且a+b+c=94,ab+bc+ac=2075,abc的值为:
已知在三角形ABC中,AB=1,AC=2,∠CAB=π/3,则三角形ABC的面积等于()
记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。



 使用微信扫一扫登录
使用微信扫一扫登录