f(x)在xo处可导是f(x)在点xo处可微的( ).
A. 充分条件
B. 必要条件
C. 充要条件
D. 无关条件
查看答案
相关试题
换一换


f(x)在xo处可导是f(x)在点xo处可微的( ).
A.充分条件 B.必要条件 C.充要条件 D.无关条件
答案
函数在点处是否可导?为什么?
答案
可导与可微的关系是:可导必可微,可微必可导,可导与可微等价
答案
下列函数中,在点x=0处可导的是()
A.y=|tanx| B.y=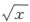 C.y=tanx2 D.y=
C.y=tanx2 D.y=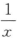
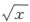 C.y=tanx2 D.y=
C.y=tanx2 D.y=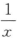
答案
设函数f(x)在点x=a处可导,则函数|f(x)|在点x=a处不可导的充分条件是( )
A.f(a)=0且f′(a)=0 B.f(a)=0且f′(a)≠0 C.f(a)>0且f′(a)> D.f(a)<0且f′(a)<
答案
f(x)在xo连续,则在xo一定可导。
答案
下列函数中在点x0=0处可导的是()。
A.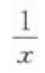 B.|x| C.
B.|x| C.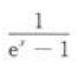 D.|x|2
D.|x|2
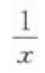 B.|x| C.
B.|x| C.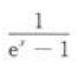 D.|x|2
D.|x|2 答案
y=fx在点x0连续,则y=fx在点x0必定可导()
答案
函数f(x)在点x=x0处连续是f(x)在点x=x0处可微的( )。
A.充分条件 B.充要条件 C.必要条件 D.无关条件
答案
函数f(x)在点x=x0处连续是它在点x=x0处可微的()条件.()
A.必要不充分 B.充分不必要 C.充分必要 D.无关
答案
热门试题
函数f(x)在点x=x0处连续是f(x)在x0处可导的( )
函数y=f'(x)在点x0处可导是函数f(x)在点x0处连续的()。
设f(x)在x=a处可导,则①|f(x)|在x=a处可导;②|f(x)|在x=a处连续;③f(x)f′(x)在x=a处连续;④[f(x)]2在x=a处可导。四个命题中正确的有( )。
若f(x)在x0点可导,则|f(x)|在点x0点处( )。
若f(x)在x0点可导,则|f(x)|在点x0点处( ).
若函数z=f(x,y)在点处可微,则下面结论中错误的是()
下列函数在x=0处可导的是( ).
函数y=f(x)在点x0处可导的充分必要条件是()。
函数在点x=a处可导,求极限/ananas/latex/p/2154/ananas/latex/p/532005
函数z=f(x,y)在点(x,y)处的偏导数存在是函数在该点可微的()
下列函数中,在x=0处可导的是()
已知下列命题:
命题A:函数f(x)在点x0处可导;
命题B:函数f(x)在点x0处可微;
命题C:函数f(z)在点x0处连续;
命题D:函数f(z)在点x0处极限存在;
命题E:函数f(工)在点x0处有定义.
试给出以上五个命题之间的相互推导关系.
设函数f(x)=|x3-1|φ(x),其中φ(x)在点x=1处连续,则φ(1)=0是f(x)在点x=1处
可导的()
若z=f(x,y)在点(x0,y0)处可微,则在点(x0,y0)处,下列结论不正确的是()
设y=f(x)在点x=0处可导,且x=0为f(x)的极值点,则f’(0)=()。
函数可微必可导。 ( )
函数可导则一定可微
二元函数z=f(x,y)在点(x0,y0)处存在一阶连续偏导数是它在此点处可微的( )。
由于函数可导与可微是等价的,故函数在一点的导数与微分是相等的.
在咬肌止点前缘处可触及()



 使用微信扫一扫登录
使用微信扫一扫登录