双曲线的实轴长为a,且此双曲线上一点P到右焦点的距离也为a,则点P到此双曲线左焦点的距离为().
A. a
B. 2a
C. 3a
D. 4a
查看答案
相关试题
换一换


双曲线的实轴长为a,且此双曲线上一点P到右焦点的距离也为a,则点P到此双曲线左焦点的距离为().
A.a B.2a C.3a D.4a
答案
已知双曲线的焦点在y轴上,且实半轴长为4、虚半轴长为5,则双曲线的标准方程为()
A.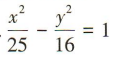 B.
B.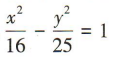 C.
C.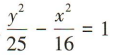 D.
D.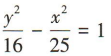
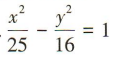 B.
B.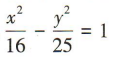 C.
C.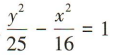 D.
D.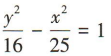
答案
已知双曲线上一点到两焦点(-5,0),(5,0)距离之差的绝对值等于6,则双曲线方程为()
A.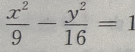 B.
B.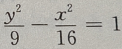 C.
C.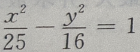 D.
D.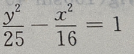
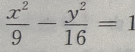 B.
B.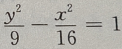 C.
C.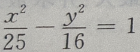 D.
D.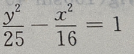
答案
已知双曲线上一点到两焦点(-5,0),(5,0)距离之差的绝对值等于6,则双曲线方程为()。
A. B.
B.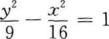 C.
C.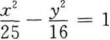 D.
D.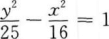
 B.
B.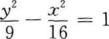 C.
C.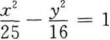 D.
D.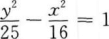
答案
已知双曲线的左、右焦点分别为F1(-3,0),F2(3,0),P为双曲线上一点且||PF1|-|PF2||=4,则双曲线的标准方程为()
A.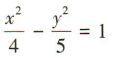 B.
B.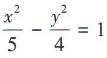 C.
C.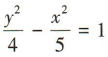 D.
D.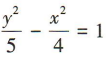
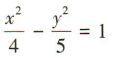 B.
B.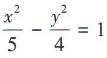 C.
C.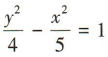 D.
D.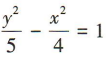
答案
双曲线的焦点一定在实轴上。()
答案
设F1和F2为双曲线的两焦点,点P在双曲线上,则||PF2|-|PF2||=()。
A.4 B.2 C.1 D.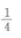
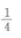
答案
求证:双曲线的一个焦点到一条渐近线的距离等于虚半轴的长.
答案
若双曲线的一个焦点坐标为F(-2,0),右顶点的坐标为(1,0),则双曲线的标准方程是()
A.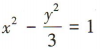 B.
B.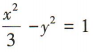 C.
C.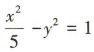 D.
D.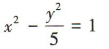
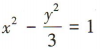 B.
B.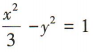 C.
C.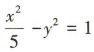 D.
D.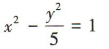
答案
已知过双曲线C:x2-y2=2右焦点的直线交双曲线于A,B两点,若A,B中点的横坐标为4,则弦AB的长为()
A.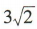 B.
B.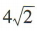 C.6 D.
C.6 D.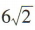
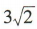 B.
B.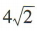 C.6 D.
C.6 D.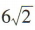
答案
热门试题
已知双曲线C:x2/a2-y2/b2=1(a>0,b>0)的一个焦点是抛物线y2=8x的焦点,且双曲线C的离心率为2,那么双曲线C的方程为_______。
共反射点时距曲线是一条双曲线,它对称于共中心点的时间轴.
过点(2,-2)且与双曲线x2-2y2=2有公共渐近线的双曲线方程是( )。
等轴双曲线过点(2,1),则它的标准方程是______。
如果双曲线的焦距为6,两条准线间的距离为4,那么双曲线的离心率为( )
焦点(-5,0)和(5,0),虚轴长是6的双曲线的标准方程是()
比能曲线是一条双曲线。
如果双曲线的焦距为6,两条准线间的距离为4,那么该双曲线的离心率为( )
中心在坐标原点,对称轴为坐标轴,且一个顶点(3,0),虚轴长为8的双曲线方程是()
已知对称轴为坐标轴的双曲线有一条渐近线的方程为2x-y=0,则双曲线的离心率为
F1、F2分别为双曲线x2/16+y2/9=1的左、右焦点,AB是双曲线左支上过F1的弦,且|AB|=3,则△ABF2的周长是()。
双曲线的一条渐近线的方程为3x+4y=0,双曲线的一个焦点为(4,0) ,则其离心率为( ).
双曲线的一条渐近线的方程为3x+4y=0,双曲线的一个焦点为(4,0),则其离心律为()
车削外圆锥时如果车刀不对中心,会产生双曲线误差,双曲线的形状是()。
采用双曲线锥齿轮的驱动桥必须要用双曲线齿轮油进行润滑。
中心在坐标原点,对称轴为坐标轴,且一个顶点为(3,0),虚轴长为8的双曲线的方程是()
双曲线y2-x2=2的焦点坐标是()
当截切平面平行正圆锥轴时,截面是双曲线()
当截切平面垂直正圆锥轴时,截面是双曲线()
当截切平面平行正圆锥轴时,截面是双曲线()



 使用微信扫一扫登录
使用微信扫一扫登录