函数f(x)=[cos(1/x)]/x在x=0点的任何邻域内都是( )。
A. 有界的
B. 无界的
C. 单调增加的
D. 单调减少的
查看答案
相关试题
换一换


函数f(x)=[cos(1/x)]/x在x=0点的任何邻域内都是( )。
A.有界的 B.无界的 C.单调增加的 D.单调减少的
答案
设三元函数xy-zlny+exz=1,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程( )。
A.只能确定一个具有连续偏导数的隐函数z=z(x,y) B.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y) C.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y) D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)
答案
二元函数在点A连续,且f(A)<0, 则必存在A的某个邻域,使得在该邻域内二元函数值恒小于0()
答案
二元函数在点A连续,且f(A)>0, 则必存在A的某个邻域,使得在该邻域内二元函数值恒大于0()
答案
如果函数f(x)在点x0的某个邻域内恒有|f(x)|≤M(M是正数),则函数f(x)在该邻域内( )。
A.极限存在 B.连续 C.有界 D.不能确定
答案
设有三元方程xy-zlny+exz=1,根据隐函数存在定理,存在点(0,1,1)的一个邻域,在此邻域内该方程()。
A.只能确定一个具有连续偏导数的隐函数z=z (x,y) B.可确定两个具有连续偏导数的隐函数x=x (y,z)和z=z(x,y) C.可确定两个具有连续偏导数的隐函数y=y (x,z)和z=z(x,y) D.可确定两个具有连续偏导数的隐函数x=x (y,z)和y=y(x,z)
答案
设函数f(x,y)在点(0,0)的某邻域内有定义,且fx(0,0)=3,fy(0,0)=-1,则有( ).
A.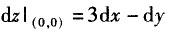 B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.
B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.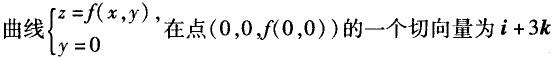 D.
D.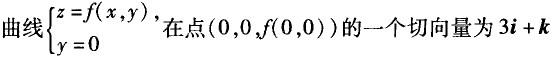
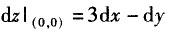 B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.
B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.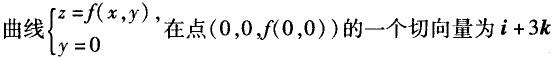 D.
D.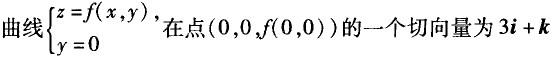
答案
设函数f(x)在点x=O的某邻域内具有连续的二阶导数,且f′(0)=f″(0)=0,则( )。
A.点x=0为f(x)的零点 B.点x=0为f(x)的极值点 C.当时,(0,f(0))为拐点 D.当时,(0,f(0))为拐点
答案
如果函数在的某邻域内都有,则在该邻域内单调递减()
A.正确 B.错误
答案
如果函数 在 的某邻域内都有 ,则 在该邻域内单调增加。()
答案
热门试题
若ƒ(x)在0某邻域(0除外)内均有ƒ(x)≥0(或ƒ(x)≤0),且函数ƒ(x)当x趋于0时极限为A,那么A≥0(或A≤()
设f(x)=(x-a)nφ(x),其中函数φ(x)在点a的某邻域内具有n-1阶导数,则f(n)(a)=____。
设f(x)=(x-a)^nφ(x),其中函数φ(x)在点a的某邻域内具有n-1阶导数,则f(n)(a)=()
设f(x)=(x-a)^nφ(x),其中函数φ(x)在点a的某邻域内具有n-1阶导数,则f(n)(a)=( )。
设?(x)在0某邻域(0除外)内均有?(x)≥0(或?(x)≤0),且函数?(x)当x趋于0时以A为极限,则A≥0(或A≤0)。(1.0分)
设函数f(x)在x=x0的某邻域内连续,在x=x0处可导,则函数f(x)|f(x)|在x=x0处()
设函数在点的某一邻域内具有连续的偏导数,且,若,则方程在点的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数,它满足条件 ,并有
下列幂函数中过点(0,0),(1,1)的偶函数是( )
试证:若函数f(x,y)的两个偏导数在点(x0,y0)的某个邻域内存在且有界,则f(x,y)在点(x0,y0)处连续。
设函数f(x)在x=a的某个邻域内连续,且f(a)为其极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有( )。
已知函数ƒ(x)=ax3-x2+bx+1(a,b∈R)在区间(-∞,0)和(1,+∞)上都是增函数,在(0,1)内是减函数. (Ⅰ)求a,b的值; (Ⅱ)求曲线y=ƒ(x)在x=3处的切线方程.
设函数fi(x)(i=1,2)具有二阶连续导数,且fi″(x0)<0(i=1,2),若两条曲线y=fi(x)(i=1,2)在点(x0,y0)处具有公切线y=g(x),且在该点处曲线y=f1(x)的曲率大于曲线y=f2(x)的曲率,则在x0的某个邻域内,有( )。
设函数f(x)在x=2的某邻域内可导,且f′(x)=ef(x),f(2)=1,则f‴(2)=____。
已知函数f(x)在区间[0,1]上连续,在区间(0,1)内可导,且f(0)=0,f(1)=1,证明:
(1)存在一点ξ∈(0,1),使得f(ξ)=1-ξ;
(2)存在两个不同的点η,ζ∈(0,1),使得f′(η)f′(ζ)=1.
设函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,k为正整数,求证:存在一点ξ∈(0,1),使得ξf′(ξ)+kf(ξ)=f′(ξ).
点x=0是函数y=arctan (1/x) 的()
函数y=cosx的图像经过点(0,1)。
设函数f(x)在(0,1)内可导,f"(x)>0,则f(x)在(0,1)内( )
设函数f(x)在区间(0,1)内可导,f’(x)>0,则在(0,1)内f(x)()。
设函数f(x)在(0,1)内可导,f'(x)>0,则f(x)在(0,1)内()。



 使用微信扫一扫登录
使用微信扫一扫登录