把抛物线 及直线 x=1 所围成的图形绕 y 轴旋转一周所得旋转体的体积为./ananas/latex/p/96601
查看答案
相关试题
换一换


把抛物线 及直线 x=1 所围成的图形绕 y 轴旋转一周所得旋转体的体积为./ananas/latex/p/96601
答案
求曲线y=x2与直线y=0,x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积.
答案
曲线y=ex(x<0),x=0,y=0所围成图形绕x轴旋转一周所得旋转体的体积为____。
答案
曲线y=e^x(x<0),x=0,y=0所围成图形绕x轴旋转一周所得旋转体的体积为( )。
A.π/2 B.π/3 C.π/4 D.π
答案
求曲线y=x2与直线y=0,x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积V.
答案
求曲线y=4x-x2和直线y=x围成的平面图形绕x轴旋转一周所得立体的体积.
答案
已知曲线y=x3(x≥0),直线x+y=2以及y轴围成一平面图形D,求平面图形D绕y轴旋转一周所得旋转体的体积.
答案
设D为曲线y=x2与直线y=x所围成的有界平面图形,求D绕x轴旋转一周所得旋转体的体积V.
答案
直线H/Rx(x≥0)与及y轴所围图形绕y轴旋转一周所得旋转体的体积为(H,R为任意常数):
A.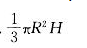 B.
B.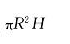 C.
C.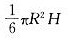 D.
D.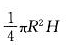
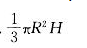 B.
B.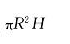 C.
C.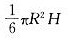 D.
D.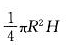
答案
曲线y=e-x (x≥0)与直线x=0,y=0所围图形绕ox轴旋转一周所得旋转体的体积为( )。
A.π/2 B.π C.π/3 D.π/4
答案
热门试题
已知曲线x=y+ey,直线x=y,y=1,y=2围成一平面图形D,求平面图形D绕y轴旋转一周所得的旋转体的体积Vy.
(1)求曲线Y=ex及直线x=1,x=0,y=0所围成的平面图形(如图3—3所示)的面积A.(2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.
设直线y=ax与抛物线y=x2所围成图形的面积为S1,它们与直线x=1所围成图形的面积为S2,并且a<1.
(1)试确定a的值,使S1+S2达到最小,并求出最小值;
(2)求该最小值所对应的平面图形绕x轴旋转一周所得旋转体的体积.
求曲线y=sinx、y=cosx、直线x=0在第一象限所围图形的面积A及该图形绕x轴旋转一周所得旋转体的体积Vx。
(1)求在区间[0,π]上的曲线y=sinx与x轴所围成图形的面积A;(2)求(1)中的平面图形绕x轴旋转一周所得旋转体的体积Vx.
由曲线y=x3,直线x=1和Ox轴所围成的平面图形绕Ox轴旋转一周所形成的旋转体的体积是( )。
设D为由曲线y=x2,y=0,x=2所围成的图形.
(1)求D的面积;
(2)求D绕x轴旋转一周所得旋转体的体积.
①求由曲线y=x,y=1/x,x=2与y=0所围成的平面图形的面积S;②求①中的平面图形绕x轴旋转一周所得旋转体的体积V.
①求曲线y=ex及直线x=1,x=0,y=0所围成的图形D的面积S:②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.
①求曲线y=x2(x≥0),y=1与x=0所围成的平面图形的面积S:②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy.
设D是由直线y=x与曲线y=x3在第一象限所围成的图形.(1)求D的面积S;(2)求D绕x轴旋转一周所得旋转体的体积V。
(1)求在区间[0,π]上的曲线y=sinx与x轴所围成图形的面积S.(2)求(1)中的平面图形绕x轴旋转一周所得旋转体的体积V.
①求在区间(0,π)上的曲线y=sinx与x轴所围成图形的面积S;②求①中的平面图形绕x轴旋转一周所得旋转体的体积Vx.
已知函数(x)=-x2+2x.①求曲线y=(x)与x轴所围成的平面图形面积S;②求①的平面图形绕x轴旋转一周所得旋转体体积Vx.
求在区间[0,π]上曲线y=sinx与x轴所围平面图形绕x轴旋转一周所得旋转体的体积。
求由曲线y=x2与x=2,y=0所围成图形分别绕x轴,y轴旋转一周所生成的旋转体体积.
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·①求平面图形的面积;②求平面图形D绕x轴旋转一周所成旋转体的体积Vx.
设D为曲线y=1-x2,直线y=x+1及x轴所围成的平面区域(如图1-3-1所示)。①求平面图形的面积;②求平面图形D绕x轴旋转一周所成旋转体的体积Vx。
求抛物线y=4-x2与直线y=3x及y轴所围成的第一象限内平面图形的面积。
求由曲线y=3-x2与y=2x,y轴所围成的平面图形的面积及该封闭图形绕x轴旋转一周所成旋转体的体积。



 使用微信扫一扫登录
使用微信扫一扫登录