数列{xn}=(-1)n+(-2)n是单调无界的。()
查看答案
相关试题
换一换


数列{xn}=(-1)n+(-2)n是单调无界的。()
答案
数列{xn}=n/(n+1),它是无界的。()
答案
“对任意给定的ε∈(0,1),总存在正整数N,当n>N时,恒有|xn-a|≤2ε”是数列{xn}收敛于a的
A.充分条件但非必要条件 B.必要条件但非充分条件 C.充分必要条件 D.既非充分条件又非必要条件
答案
“对任意给定的ε∈(0,1),总存在正整数N,当n≥N时,恒有|xn-a|≤2ε”是数列{xn}收敛于a的( ).
A.充分条件但非必要条件 B.必要条件但非充分条件 C.充分必要条件 D.既非充分又非必要条件
答案
设ƒ(x)=ax-1,其中常数a>0,如果{xn}是等差数列,且xn=2n-1,
(Ⅰ)求证:{ƒ(xn)}是等比数列;
(Ⅱ)求数列{ƒ(xn)}的前n项和Sn的表达式。
(Ⅰ)求证:{ƒ(xn)}是等比数列;
(Ⅱ)求数列{ƒ(xn)}的前n项和Sn的表达式。
答案
设数列an的前n项和为Sn,则数列an是等差数列。(1)Sn=n2+2n,n=1,2,3……(2)Sn=n2+2n+1,n=1,2,3……
A.条件(1)充分,但条件(2)不充分 B.条件(2)充分,但条件(1)不充分 C.条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分 D.条件(1)充分,条件(2)充分 E.条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分
答案
已知数列{an}中,a1=1,an=2n-1.
(1)证明{an}是等差数列;
(2)求数列{an}的前n项和Sn.
答案
已知数列 {an}中,Sn是它的前n项和,并且 Sn+1=4an+2,a1=1。(Ⅰ)设 bn=an+1−2an,求证:数列{bn}是等比数列;(Ⅱ)设 cn=an/2n,求证:数列{cn}是等差数列;(Ⅲ)求数列{an}的通项公式及前n项和。
答案
若数列{an}满足a1=2,an+1-an=1,则数列{an}的通项公式an=()
A.n2+1 B.n+1 C.n-1 D.-n+3
答案
数列{an}中,若an+1=1/2an(n≥1,n∈N),且a1=2,则前5项的和是()。
A.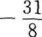 B.
B. C.
C. D.
D.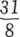
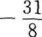 B.
B. C.
C. D.
D.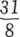
答案
热门试题
Fibonacci数列的前几个数为:0,1,1,2,3,5,…,其规律是:F1=0(n=1)、F2=1(n=2)、Fn=F(n-1)+F(n-2)(n≥3)编程求此数列的前40项之和
已知数列{an}的前n项和Sn=2n+1-k(其中k为常数): (1)求数列{an}的通项公式; (2)若a1=2,求数列{nan}的前n项和Tn。
设Sn为数列{an}的前n项和,Sn=3/2(an-1)(n∈N+),数列{bn}的通项公式为bn=4n+3(n∈N+)。(Ⅰ)求数列{an}的通项公式;(Ⅱ)若di∈{a1,a2,…,an,…}∩{b1,b2,…,bn,…}(i=1,2,…,n,…),则称数列{dn}为数列{an}与{bn}的公共项,将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新的数列(dn),证明{dn}的通项公式为dn=32n+1(n∈N)。
已知数列{an}的前n项和为Sn=-2n2-n.求证:数列的通项公式是an=1-4n.
数列{an}满足a1=1/2,a1+a2+···+an=n2·an,求an。
已知数列(an}的首项为1,an+1=2an+n-1,求数列{an}的通项公式.
已知数列{an}是等差数列,a1=1,a3=3.
(1)求数列{an}的通项公式;
(2)设bn=(-1)nan,数列{bn}的前n项和为Tn,求T100
在等比数列{an}中,a1=2,前n项和为Sn,若数列{an+1}也是等比数列,则Sn=()
求菲波那契数列的数学表达式为 fibonacci(n)=n, n=0,1; fibonacci(n)=fibonacci(n-1)+fibonacci(n-2), n≥2; 设m是long型变量,下面是递归算法求菲波那契数列的方法 long fibonacci(long n) if(n= =0| |n= =1)return n; else return (fibonacci(n-1)+fibona
数列{an}的前n项和 Sn=3n2+n+1,求该数列的通项an.
已知数列{an}中, a1=2,an+1=an+2n(n∈N*),则a10等于 ()
已知等差数列{an}的前n项和是Sn,若S2n-1=(2n-1)(2n+1),则Sn等于( )
(10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数): (1)求数列{ an }的通项公式;(4分) (2)若a1=2,求数列{n an }的前n项和Tn。(6分)
已知数列{an}的前n项和是Sn,且2Sn+an=1(n∈N*)。 (1)求证:数列{an}是等比数列; (2)记bn=10+log9an,求{bn}的前n项和Tn的最大值及相应的n值。
已知数列{an}满足:a1=2,an=2an-1-1(n≥2),求{an}的通项公式。
题目:斐波那契数列。 def fib(n): if n == 1 or n == 2: return 1 else: _________________________ print (fib(100))
已知数列{an}的前n项和为Sn,若Sn=n2+1(n∈N*),则a1+a2019=( )。
在数列{an}中,a1=4,an+1-an=2(n∈N*),则a6=()
设数列{an}的前n项和为Sn,且an+Sn=1(n∈N*)。(1)求{an}的通项公式; (2)若数列{bn}满足b1=1,且2bn+1=bn+an(n≥1),求数列{bn}的通项公式。
已知数列{an}的通项公式是an=log3(2n+1),那么2是这个数列的第()项.



 使用微信扫一扫登录
使用微信扫一扫登录