设函数ƒ(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数ƒ(x)ex的一个极值点,则下列图像不可能为ƒ(x)的图象的是()
A. 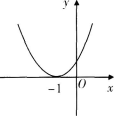 B.
B. 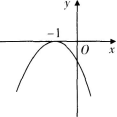 C.
C. 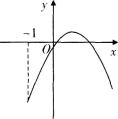 D.
D. 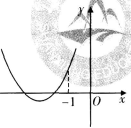




查看答案
相关试题
换一换


设f(x)的一个原函数为xex,则∫xf′(x)dx=____。
答案
设函数f(x)=kx,若f(1)=-2,则( )。
A.k=1 B.k=-2 C.k=-1 D.k=2
答案
设f(x)=xex,则函数f(n)(x)在x=____处取最小值____.
答案
设函数f(x)在(a,b)内连续,a<x1<x2<…<xn<b,证明:必∃ξ∈(a,b),使f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。
答案
设二元函数z=xex+y+(x+1)ln(1+y),则dz|(1,0)____.
答案
设F(x)是随机变量X的分布函数,则对()随机变量X,有P{x1 < X < x2}=F(x1) – F(x2)
A.任意 B.连续型 C.离散型 D.个别离散型
答案
若函数f(x)对任意实数x1、x2均满足关系式f(x1+x2)=f(x1)f(x2)。且f′(0)=2,则必有( )
A.f(0)=0 B.f(0)=2 C.f(0)=1 D.f(0)=-1
答案
求函数y=x1?
答案
设函数f(x)=x1nx
(1)画出函数f(x)的草图。(6分)
(2)若
的最大值(提示利用函数f(x)的凸性)。
答案
函数 y=x1/2的定义域是()
A.[2,+∞) B.[0,+∞) C.(-∞,0) D.(0,+∞)
答案
热门试题
设函数f(x)=a2x-1+5,若f(2)=13,则f(-1)=()
如果X的分布函数为F(x), 则对任意实数x1 < x2 ,有P{ x1 < x2 }=F(x2) – F(x1)()
一个关系模式为Y(X1,X2,X3,X4),假定该关系存在如下函数依赖:X1→X2,X1→X3,X3→X4,则该关系属于 【1】 范式,因为它存在着 【2】 函数依赖
若函数f(x)在区间(a,b)内可导,x1和x2是区间(a,b)内任意两点(x1<x2),则至少存在一点ξ,使( )
函数y=C1ex+C2e-2x+xex满足的一个微分方程是( )。
设f(x)是[0,1]上的可导函数,且f′(x)有界。证明:存在M>0,使得对于任意x1,x2∈[0,1],有|f(x1)-f(x2)|≤M|x1-x2|。
若函数f(x)=2x+a-1(x∈R)为奇函数,则f(-1)=()
中国大学MOOC: 如果X的分布函数为F(x), 则对任意实数x1 < x2 ,有P{ x1 < X< x2 }=F(x2) – F(x1).
设函数f(x)=x1nx (1)画出函数f(x)的草图。(6分) (2)若的最大值(提示利用函数f(x)的凸性)。(4分)
设 f(x)是[0,1]上的可导函数,且厂 f"(x)有界。证明:存在 M>0,使得对于任意 x1,x2∈[0,1],有|f(x1)-f(x2)| ≤M|x1-x2|。
已知函数f(x)=(x-m)2+2.
(1)若函数f(x)的图像过点(2,2),求函数y=f(x)的单调递增区间;
(2)若函数f(x)是偶函数,求m的值
设函数(x)=1+sin2x,求"(0).
设函数ƒ(x)=1+sin2x,求ƒ'(0)。
设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数,则a与b分别是:()
已知二次函数y=ax2+bx+c(a>0)的图象经过(0,1),(4,0),当该二次函数的自变量分别取x1,x2(0<x1<x2<4)时,对应的函数值是y1,y2,且y1=y2,设该函数图象的对称轴是x=m,则m的取值范围是()
设随机变量X仅取n个值x1, x2,… xn,其概率函数为P(X=xi)=pi,则( )。
设随机变量X仅取n个值x1, x2,… xn,其概率函数为P(X=xi)=pi,则( )。
设函数ƒ(x)=1-ƒ(x)log2x,则ƒ(2)=()。
设函数f(x十1)=2x+2,则f(x)=()
设函数f(x-2)=x^2+1,则f(x+1)=()



 使用微信扫一扫登录
使用微信扫一扫登录