数列1,4,9,16,25,……的通项公式为
查看答案
相关试题
换一换


已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为( )
A.248 B.168 C.128 D.19 E.以上选项均不正确
答案
数列9,99,999,9999,....的通项公式为_____。
答案
一阶线性非齐次递归数列不能求出该数列通项公式
答案
数列{an}是首项为-2的等差数列,若a₂+a₃=8,则{an}的通项公式是()
A.an=4n-6 B.an=4n-2 C.an=-4n-2 D.an=-4n+2
答案
数列1,4,9,16,25,……的通项公式为
答案
数列{an}的通项公式an=3n+2,则此数列是( )
A.公差为2的等差数列 B.公差为3的等差数列 C.首项为2的等差数列 D.不是等差数列
答案
若数列{an}的通项公式为an=-n+5,则该数列是()
A.公差为-1的等差数列 B.公差为5的等差数列 C.首项为5的等差数列 D.公差为n的等差数列
答案
设数列{an}的前n项和为Sn,且an+Sn=1(n∈N*)。(1)求{an}的通项公式; (2)若数列{bn}满足b1=1,且2bn+1=bn+an(n≥1),求数列{bn}的通项公式。
答案
数列3,7,13,21,31,…的一个通项公式是()
A.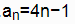 B.
B. C.
C. D.
D.
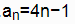 B.
B. C.
C. D.
D.
答案
已知等差数列{an}的前三项为a-1,a+1,2a+3,则此数列的通项公式为( ).
A.an=2n-5 B.an=2n+1 C.an=2n-3 D.an=2n-1
答案
热门试题
已知数列{an}的通项公式为an=-2n+3,写出该数列的前5项.
数列1,0,1,0,1,0,…的一个通项公式是().
等差数列{an}的通项公式为an=3n-1,在{an}中,每相邻的两项之间插人三项,构成新的等差数列{bn}. (Ⅰ)求{bn}的通项公式; (Ⅱ)求{bn}前10项的和.
等差数列{an}前三项分别为a-1,a+1,a+3,则该数列的通项公式为()
数列的通项公式是an=n(2n+1),则它的第7项是()
已知数列{an}的通项公式是an=log3(2n+1),那么2是这个数列的第()项.
已知数列通项公式为an=n+2,那么它的第4项a4=28。()
设Sn为数列{an}的前n项和,Sn=3/2(an-1)(n∈N+),数列{bn}的通项公式为bn=4n+3(n∈N+)。(Ⅰ)求数列{an}的通项公式;(Ⅱ)若di∈{a1,a2,…,an,…}∩{b1,b2,…,bn,…}(i=1,2,…,n,…),则称数列{dn}为数列{an}与{bn}的公共项,将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新的数列(dn),证明{dn}的通项公式为dn=32n+1(n∈N)。
已知数列(an}的首项为1,an+1=2an+n-1,求数列{an}的通项公式.
在等差数列{an}中,a2=4,公差d=2,求数列{an}的通项公式及前n项和Sn。
(10分)已知数列{an}满足a1=3,an+1= an +2n, (1)求{ an }的通项公式an; (2)若bn=n an,求数列{bn}的前n项和sn。
已知数列{an}的前n项和Sn=n2-2n.求(1){an}的前三项;(2){an}的通项公式.
(10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数): (1)求数列{ an }的通项公式;(4分) (2)若a1=2,求数列{n an }的前n项和Tn。(6分)
若数列{an}满足a1=2,an+1-an=1,则数列{an}的通项公式an=()
在等比数列{an}中,a2=2,a5=16.
(1)求首项a1和公比q,并写出{an}的通项公式;
(2)求数列{an}的前7项和S7
在等比数列{an}中, a5=1/2,a8=−1/16,求通项公式.
已知{an}是等差数列,且a2=-2,a4=-1. (Ⅰ)求{an}的通项公式; (Ⅱ)求{an}的前n项和Sn.
针对“等差数列”的教学,某教师制定了如下教学目标。目标一:理解等差数列的概念,掌握等差数列的通项公式;目标二:理解等差数列通项公式的推导方法,会运用等差数列的通项公式解决实际问题;目标三:通过公式的推导过程,培养观察、分析、归纳能力和严密的逻辑思维能力。(1)针对“等差数列”的内容,回答下列问题:①分析学生已有的知识基础;②设计一个等差数列的教学引人片段,并说明设计意图。(2)请针对上述教学目标,完成下列任务:①根据教学目标一、二,设计一个习题,帮助学生理解等差数列,并说明设计意图;②根据教学目标二、三,设计推导等差数列通项公式的教学片段,并说明设计意图。
已知数列(an}的通项公式为an=n2-8n+15,则3与数列{an}的关系是().
已知数列0,3,8,15,24...,则它的一个通项公式为an=n2-1。()



 使用微信扫一扫登录
使用微信扫一扫登录